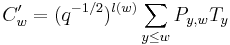Iwahori–Hecke algebra
In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group.
Hecke algebras are quotients of the group rings of Artin braid groups. This connection found a spectacular application in Vaughan Jones' construction of new invariants of knots. Representations of Hecke algebras led to discovery of quantum groups by Michio Jimbo. Michael Freedman proposed Hecke algebras as a foundation for topological quantum computation.
Contents |
Hecke algebras of Coxeter groups
Definitions
There are several definitions of Hecke algebras in the literature which are more or less general.
Suppose for the following definitions that (W,S) is a Coxeter system with the Coxeter matrix M and R is a commutative ring with identity.
Multiparameter Hecke algebras
If 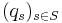 is a family of units of
is a family of units of  such that
such that 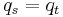 whenever
whenever  and
and  are conjugate in
are conjugate in  , then define the multiparameter Hecke algebra
, then define the multiparameter Hecke algebra 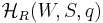 as the unital, associative
as the unital, associative  -algebra with generators
-algebra with generators 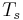 for all
for all 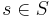 and the relations:
and the relations:
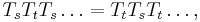 where each side has
where each side has 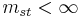 factors and
factors and 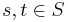 (braid relations)
(braid relations)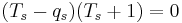 for all
for all 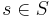 (quadratic relation).
(quadratic relation).
If  is the ring
is the ring ![A:=\mathbb{Z}[q_s^{\pm 1} | s\in S]](/2012-wikipedia_en_all_nopic_01_2012/I/8ef435e962cef6f0e109aed0798929d2.png) of Laurent Polynomials over
of Laurent Polynomials over  with indeterminants
with indeterminants 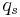 (and the above restriction that
(and the above restriction that 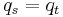 whenever
whenever  and
and  are conjugated), then one calls the above Hecke algebra the generic multiparameter Hecke algebra.
are conjugated), then one calls the above Hecke algebra the generic multiparameter Hecke algebra.
The generic algebra is universal in the sense that every other multiparameter Hecke algebra can be obtained from it via the (unique) ring homomorphism ![A=\mathbb{Z}[q_s^{\pm1}]\to R](/2012-wikipedia_en_all_nopic_01_2012/I/49b94dd64098c1338413eb3bbc46b94d.png) which maps the indeterminant
which maps the indeterminant 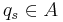 to the unit
to the unit 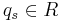 . This homomorphism turns
. This homomorphism turns  into a
into a  -algebra and the scalar extension
-algebra and the scalar extension 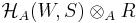 is canonically isomorphic to the Hecke algebra
is canonically isomorphic to the Hecke algebra 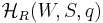 as constructed above. One calls this process specialization of the generic algebra.
as constructed above. One calls this process specialization of the generic algebra.
Warning: in recent books and papers, Lusztig has been using a modified form of the quadratic relation that reads 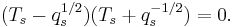 After extending the scalars to include the half integer powers
After extending the scalars to include the half integer powers 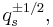 the resulting Hecke algebra is isomorphic to the previously defined one (but the
the resulting Hecke algebra is isomorphic to the previously defined one (but the 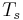 here corresponds to
here corresponds to 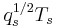 in our notation). While this does not change the general theory, many formulas look different.
in our notation). While this does not change the general theory, many formulas look different.
Coxeter groups with weights
If an integral weight function is defined on  (i.e. a map
(i.e. a map 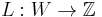 with
with 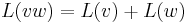 for all
for all 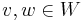 with
with 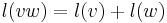 ), then a common specialization to look at is the one induced by the homomorphism
), then a common specialization to look at is the one induced by the homomorphism 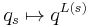 , where
, where  is a single indeterminant over
is a single indeterminant over  .
.
If one uses the convention with half-integer powers, then weight function 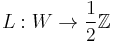 may be permitted as well. For technical reasons it is also often convenient only to consider positive weight functions.
may be permitted as well. For technical reasons it is also often convenient only to consider positive weight functions.
One-parameter Hecke algebras
If one specializes every indeterminant 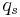 to a single indeterminant
to a single indeterminant  over the integers (or
over the integers (or 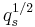 to
to 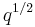 respectively), then one obtains the so called generic one-parameter Hecke algebra of
respectively), then one obtains the so called generic one-parameter Hecke algebra of 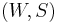 .
.
Since in Coxeter groups with single laced Dynkin diagrams (for example groups of type A and D) every pair of Coxeter generators is conjugated, the above mentioned restriction of 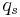 being equal
being equal  whenever
whenever  and
and  are conjugated in
are conjugated in  forces the multiparameter and the one-parameter Hecke algebras to be equal. Therefore it is also very common to only look at one-parameter Hecke algebras.
forces the multiparameter and the one-parameter Hecke algebras to be equal. Therefore it is also very common to only look at one-parameter Hecke algebras.
Properties
1. The Hecke algebra has a basis 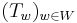 over
over  indexed by the elements of the Coxeter group
indexed by the elements of the Coxeter group  . In particular,
. In particular,  is a free
is a free  -module. If
-module. If 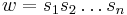 is a reduced decomposition of
is a reduced decomposition of  , then
, then 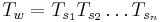 . This basis of Hecke algebra is sometimes called the natural basis. The neutral element of
. This basis of Hecke algebra is sometimes called the natural basis. The neutral element of  corresponds to the identity of
corresponds to the identity of  :
: 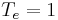 .
.
2. The elements of the natural basis are multiplicative, namely, 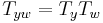 whenever
whenever 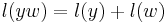 , where
, where 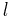 denotes the length function on the Coxeter group
denotes the length function on the Coxeter group  .
.
3. Elements of the natural basis are invertible. For example, from the quadratic relation we conclude that 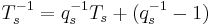 .
.
4. Suppose that  is a finite group and the ground ring is the field
is a finite group and the ground ring is the field  of complex numbers. Jacques Tits has proved that if the indeterminate
of complex numbers. Jacques Tits has proved that if the indeterminate  is specialized to any complex number outside of an explicitly given list (consisting of roots of unity), then the resulting one parameter Hecke algebra is semisimple and isomorphic to the complex group algebra
is specialized to any complex number outside of an explicitly given list (consisting of roots of unity), then the resulting one parameter Hecke algebra is semisimple and isomorphic to the complex group algebra ![\mathbb{C}[W]](/2012-wikipedia_en_all_nopic_01_2012/I/f3211f3b114d6fc547da3a238d069742.png) (which also corresponds to the specialization
(which also corresponds to the specialization 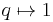 ).
).
5. More generally, if  is a finite group and the ground ring
is a finite group and the ground ring  is a field of characteristic zero, then the one parameter Hecke algebra is a semisimple associative algebra over
is a field of characteristic zero, then the one parameter Hecke algebra is a semisimple associative algebra over ![R[q^{\pm 1}]](/2012-wikipedia_en_all_nopic_01_2012/I/81672143d93e99ec98ac252bbf970ee9.png) . Moreover, extending earlier results of Benson and Curtis, George Lusztig provided an explicit isomorphism between the Hecke algebra and the group algebra after the extension of scalars to the quotient field of
. Moreover, extending earlier results of Benson and Curtis, George Lusztig provided an explicit isomorphism between the Hecke algebra and the group algebra after the extension of scalars to the quotient field of ![R[q^{\frac12}].](/2012-wikipedia_en_all_nopic_01_2012/I/def9cd088eef9ae1d05570743c9bde98.png)
Canonical basis
A great discovery of Kazhdan and Lusztig was that a Hecke algebra admits a different basis, which in a way controls representation theory of a variety of related objects.
Consider a Hecke algebra 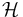 over the ring
over the ring ![A=\mathbb{Z}[q^{\frac12},q^{-\frac12}],](/2012-wikipedia_en_all_nopic_01_2012/I/1afb8940e4825ac0d0e110105f5380a4.png) as above. This ring has an involution bar that maps
as above. This ring has an involution bar that maps 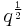 to
to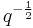 and acts as identity on
and acts as identity on  . Then
. Then  admits a unique ring automorphism
admits a unique ring automorphism  that is semilinear with respect to the bar involution of
that is semilinear with respect to the bar involution of  and maps
and maps  to
to 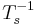 . It can further be proved that this automorphism is involutive (has order two) and takes any
. It can further be proved that this automorphism is involutive (has order two) and takes any 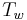 to
to 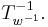
Theorem (Kazhdan–Lusztig)
For each 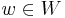 there exists a unique element
there exists a unique element 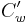 which is invariant under the involution
which is invariant under the involution  and has the property that in the expansion
and has the property that in the expansion
over the elements of the natural basis, one has ![P_{w,w}=1, P_{y,w}(q) \in \mathbb{Z}[q]](/2012-wikipedia_en_all_nopic_01_2012/I/2ab5b240e31e18acbb07fc1ed6d224ba.png) has degree
has degree 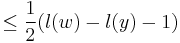 if
if 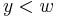 in the Bruhat order and
in the Bruhat order and 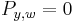 if
if 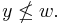
The elements 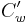 where
where  varies over
varies over  form a basis of the algebra
form a basis of the algebra  , which is called the dual canonical basis of the Hecke algebra
, which is called the dual canonical basis of the Hecke algebra  . The canonical basis
. The canonical basis 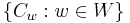 is obtained in a similar way. The polynomials
is obtained in a similar way. The polynomials 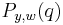 making appearance in this theorem are the Kazhdan–Lusztig polynomials.
making appearance in this theorem are the Kazhdan–Lusztig polynomials.
The Kazhdan–Lusztig notions of left, right and two-sided cells in Coxeter groups are defined through the behavior of the canonical basis under the action of 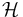 .
.
Hecke algebra of a locally compact group
Iwahori–Hecke algebras first appeared as an important special case of a very general construction in group theory. Let (G,K) be a pair consisting of a unimodular locally compact topological group G and a closed subgroup K of G. Then the space of bi-K-invariant continuous functions of compact support
- C[K\G/K]
can be endowed with a structure of an associative algebra under the operation of convolution. This algebra is denoted
- H(G//K)
and called the Hecke ring of the pair (G,K). If we start with a Gelfand pair then the resulting algebra turns out to be commutative. In particular, this holds when '
- G = SLn(Qp) and K = SLn(Zp)
and the representations of the corresponding commutative Hecke ring were studied by Ian G. Macdonald.
On the other hand, in the case
- G = SL2(Q) and K = SL2(Z)
we arrive at the abstract ring behind Hecke operators in the theory of modular forms, which gave the name to Hecke algebras in general.
The case leading to the Hecke algebra of a finite Weyl group is when G is the finite Chevalley group over a finite field with pk elements, and B is its Borel subgroup. Iwahori showed that the Hecke ring
- H(G//B)
is obtained from the generic Hecke algebra Hq of the Weyl group W of G by specializing the indeterminate q of the latter algebra to pk, the cardinality of the finite field. George Lusztig remarked in 1984 (Characters of reductive groups over a finite field, xi, footnote):
- I think it would be most appropriate to call it the Iwahori algebra, but the name Hecke ring (or algebra) given by Iwahori himself has been in use for almost 20 years and it is probably too late to change it now.
Iwahori and Matsumoto (1965) considered the case when G is a group of points of a reductive algebraic group over a non-archimedean local field K, such as Qp, and K is what is now called an Iwahori subgroup of G. The resulting Hecke ring is isomorphic to the Hecke algebra of the affine Weyl group of G, or the affine Hecke algebra, where the indeterminate q has been specialized to the cardinality of the residue field of K.
Work of Roger Howe in the 1970s and his papers with Allen Moy on representations of p-adic GLn opened a possibility of classifying irreducible admissible representations of reductive groups over local fields in terms of appropriately constructed Hecke algebras. (Important contributions were also made by Joseph Bernstein and Andrey Zelevinsky.) These ideas were taken much further in Colin Bushnell and Philip Kutzko's theory of types, allowing them to complete the classification in the general linear case. Many of the techniques can be extended to other reductive groups, which remains an area of active research. It has been conjectured that all Hecke algebras that are ever needed are mild generalizations of affine Hecke algebras.
Representations of Hecke algebras
It follows from Iwahori's work that complex representations of Hecke algebras of finite type are intimately related with the structure of the spherical principal series representations of finite Chevalley groups.
George Lusztig pushed this connection much further and was able to describe most of the characters of finite groups of Lie type in terms of representation theory of Hecke algebras. This work used a mixture of geometric techniques and various reductions, led to introduction of various objects generalizing Hecke algebras and detailed understanding of their representations (for q not a root of unity). Modular representations of Hecke algebras and representations at roots of unity turned out to be related with the theory of canonical bases in affine quantum groups and very interesting combinatorics.
Representation theory of affine Hecke algebras was developed by Lusztig with a view towards applying it to description of representations of p-adic groups. It is in many ways quite different in flavor from the finite case. A generalization of affine Hecke algebras, called double affine Hecke algebra, was used by Ivan Cherednik in his proof of the Macdonald conjectures.
References
- David Goldschmidt Group Characters, Symmetric Functions, and the Hecke Algebra ISBN 0-8218-3220-4
- Iwahori, Nagayoshi; Matsumoto, Hideya On some Bruhat decomposition and the structure of the Hecke rings of p-adic Chevalley groups. Publications Mathématiques de l'IHÉS, 25 (1965), pp. 5–48
- Alexander Kleshchev, Linear and projective representations of symmetric groups, Cambridge tracts in mathematics, vol. 163. Cambridge University Press, 2005. ISBN 0 521 83703 0
- George Lusztig, Hecke algebras with unequal parameters, CRM monograph series, vol.18, American Mathematical Society, 2003. ISBN 0-8218-3356-1
- Andrew Mathas, Iwahori-Hecke algebras and Schur algebras of the symmetric group, University Lecture Series, vol.15, American Mathematical Society, 1999. ISBN 0-8218-1926-7
- Lusztig, George, On a theorem of Benson and Curtis, J. Algebra 71 (1981), no. 2, 490–498. doi:10.1016/0021-8693(81)90188-5
- Colin Bushnell and Philip Kutzko, The admissible dual of GL(n) via compact open subgroups, Annals of Mathematics Studies, vol. 129, Princeton University Press, 1993. ISBN 0-691-02114-7