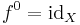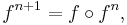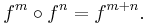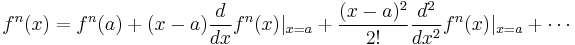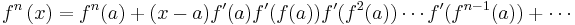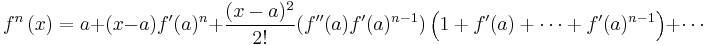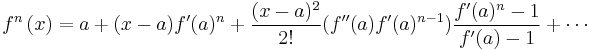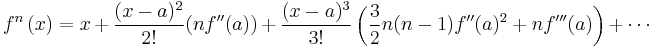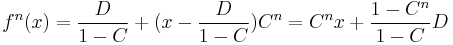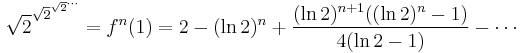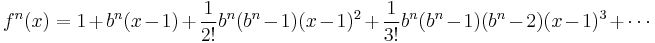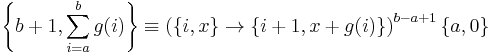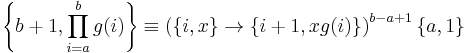Iterated function

In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated. The sequence of numbers that is obtained from this process is called an orbit.

Iterated functions are objects of study in computer science, fractals, and dynamical systems.

1 Definition
2 Abelian property and Iteration sequences
3 Fixed points
4 Limiting behaviour
5 Fractional iterates and flows
6 Formulae for fractional iteration
7 Conjugacy
8 Markov chains
9 Examples
10 Means of study
11 In computer science
12 Definitions in terms of Iterated Functions
13 See also
14 References

Definition

The formal definition of an iterated function on a set X follows:

Let X be a set and f:X → X be a function.

Define 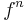$f^n\,$ as the n-th iterate of f, where n is a non-negative integer, by:

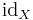$f^0=\operatorname{id}_X\,$

and

$f^{n%2B1} = f \circ f^{n},\,$

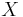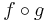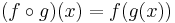where $\operatorname{id}_X\,$ is the identity function on $X\,$ and $f \circ g\,$ denotes function composition; that is, $(f \circ g)(x)=f(g(x))$ .

Abelian property and Iteration sequences

In general, the following identity holds for all non-negative integers m and n,

$f^{m} \circ f^{n} = f^{m%2Bn}.\,$

This is structurally identical to the property of exponentiation that 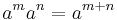$a^{m} a^{n} = a^{m%2Bn}$ , i.e. the special case f(x)=ax.

In general, for arbitrary general (negative, non-integer, etc.) indices m and n, this relation is called the translation functional equation, cf. Schröder's equation. On a logarithmic scale, this reduces to the nesting property of Chebyshev polynomials, T_m(T_n(x))=T_{m n}(x).

Because the notation 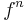$f^n\,$ may refer to both iteration (composition) of the function 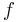$f\,$ and exponentiation of the function 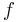$f\,$ , some mathematicians choose to write 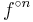$f^{\circ n}\,$ for the n-th iterate of the function $f\,$ .

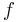The sequence of functions 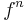$f^n \,$ is called a Picard sequence,^[1]^[2] named after Charles Émile Picard.

For a given x in X, the sequence of values 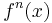$f^n(x) \,$ is called the orbit of x.

If $f^n(x) \,= f^{n%2Bm} \,(x)$ for some integer m, the orbit is called a periodic orbit. The smallest such value of m for a given x is called the period of the orbit. The point x itself is called a periodic point. The cycle detection problem in computer science is the algorithmic problem of finding the first periodic point in an orbit, and the period of the orbit.

Fixed points

If f(x) = x for some x in X, then x is called a fixed point of the iterated sequence. The set of fixed points is often denoted as Fix(f). There exist a number of fixed-point theorems that guarantee the existence of fixed points in various situations, including the Banach fixed point theorem and the Brouwer fixed point theorem.

There are several techniques for convergence acceleration of the sequences produced by fixed point iteration. For example, the Aitken method applied to an iterated fixed point is known as Steffensen's method, and produces quadratic convergence.

Limiting behaviour

Upon iteration, one may find that there are sets that shrink and converge towards a single point. In such a case, the point that is converged to is known as an attractive fixed point. Conversely, iteration may give the appearance of points diverging away from a single point; this would be the case for an unstable fixed point.^[3] When the points of the orbit converge to one or more limits, the set of accumulation points of the orbit is known as the limit set or the ω-limit set.

The ideas of attraction and repulsion generalize similarly; one may categorize iterates into stable sets and unstable sets, according to the behaviour of small neighborhoods under iteration.

Other limiting behaviours are possible; for example, wandering points are points that move away, and never come back even close to where they started.

Fractional iterates and flows

In some instances, fractional iteration of a function can be defined: for instance, a half iterate of a function f is a function g such that g(g(x)) = f(x). This idea can be generalized so that the iteration count n becomes a continuous parameter; in this case, such a system is called a flow, specified by Schröder's equation. (cf. Section on #Conjugacy below.)

Formulae for fractional iteration

One method of finding a series formula for fractional iteration, making use of a fixed point, is as follows.

(1) First determine a fixed point for the function such that f(a)=a.

(2) Define 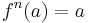$f^n(a)=a$ for all n belonging to the reals. This in some ways is the most natural extra condition to place upon the fractional iterates.

(3) Expand 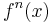$f^n(x)$ around the fixed point a as a Taylor series.

$f^n(x) = f^n(a) %2B (x-a)\frac{d}{dx}f^n(x)|_{x=a} %2B \frac{(x-a)^2}{2!}\frac{d^2}{dx^2}f^n(x)|_{x=a} %2B\cdots$

(4) Expand out:

$f^n\left(x\right) = f^n(a) %2B (x-a) f'(a)f'(f(a))f'(f^2(a))\cdots f'(f^{n-1}(a)) %2B \cdots$

(5) Substitute in for 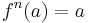$f^n(a)=a$ :

$f^n\left(x\right) = a %2B (x-a) f'(a)^{n} %2B \frac{(x-a)^2}{2!}(f''(a)f'(a)^{n-1})\left(1%2Bf'(a)%2B\cdots%2Bf'(a)^{n-1} \right)%2B\cdots$

(6) Make use of geometric progression to simplify terms.

$f^n\left(x\right) = a %2B (x-a) f'(a)^{n} %2B \frac{(x-a)^2}{2!}(f''(a)f'(a)^{n-1})\frac{f'(a)^n-1}{f'(a)-1}%2B\cdots$

(6b) There is a special case when f'(a)=1:

$f^n\left(x\right) = x %2B \frac{(x-a)^2}{2!}(n f''(a))%2B \frac{(x-a)^3}{3!}\left(\frac{3}{2}n(n-1) f''(a)^2 %2B n f'''(a)\right)%2B\cdots$

(7) When n is not an integer we make use of the power formula 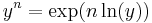$y^n = \exp(n \ln(y))$

This can be carried on indefinitely although the latter terms become increasingly complicated.

Example 1

For example setting 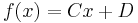$f(x) = Cx%2BD$ gives the fixed point 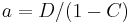$a = D/(1-C)$ and the formula above gives:

$f^n(x) = \frac{D}{1-C} %2B (x-\frac{D}{1-C})C^n = C^n x %2B \frac{1-C^n}{1-C}D$

which is the correct formula. The next terms are all zero as they contain higher derivatives.

Example 2

We want to find the value of 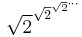$\sqrt{2}^{ \sqrt{2}^{\sqrt{2}^{\cdots}} }$ where this is done n times (and perhaps the interpolated values when n is not an integer). We have 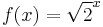$f(x)=\sqrt{2}^x$ . A fixed point is 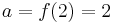$a=f(2)=2$ . So set x=1 and 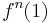$f^n(1)$ expanded around the value of 2 is then an infinite series:

$\sqrt{2}^{ \sqrt{2}^{\sqrt{2}^{\cdots}} } = f^n(1) = 2 - (\ln 2)^n %2B \frac{(\ln 2)^{n%2B1}((\ln 2)^n-1)}{4(\ln 2-1)} - \cdots$

which taking just the first three terms is correct to the first decimal place when n is positive. (Using the other fixed point 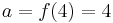$a=f(4)=4$ causes the series to diverge.)

Example 3

When n=-1 this series computes the inverse function.

Example 4

With the function 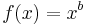$f(x)=x^b$ we expand around the fixed point 1 to get the series:

$f^n(x) = 1 %2B b^n(x-1) %2B \frac{1}{2!}b^{n}(b^n-1)(x-1)^2 %2B \frac{1}{3!}b^n (b^n-1)(b^n-2)(x-1)^3 %2B \cdots$

which is simply the Taylor series of 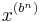$x^{(b^n)}$ expanded around 1.

Conjugacy

If f and g are two iterated functions, and there exists a homeomorphism h such that 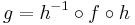$g=h^{-1} \circ f \circ h$ , then f and g are said to be topologically conjugate. Clearly, topological conjugacy is preserved under iteration, as one has that 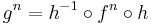$g^n=h^{-1}\circ f^n \circ h$ , so that if one can solve one iterated function system, one has solutions for all topologically conjugate systems. For example, the tent map is topologically conjugate to the logistic map.

Even in the absence of a strict homeomorphism, near a fixed point, here taken to be at x=0, f(0)=0, one may often solve^[4] Schröder's equation for a function Ψ, which makes f(x) locally conjugate to f '(0)x. Thus, its iteration orbit, or flow, under suitable provisions (e.g., f '(0) ≠1), amounts to the conjugate of the orbit of the monomial, Ψ⁻¹(f '(0)ⁿ Ψ(x)). Here, however, n no longer needs be integer or positive, and is a continuous "time" of evolution for the full orbit^[5]: the semigroup of the Picard sequence has generalized to a full continuous group. This is evidently equivalent to the algorithm of the preceding section, albeit more powerful and systematic.

Markov chains

If the function can be described by a stochastic matrix, that is, a matrix whose rows or columns sum to one, then the iterated system is known as a Markov chain.

Examples

Famous iterated functions include the Mandelbrot set and Iterated function systems.

Ernst Schröder,^[6] in 1870, worked out special cases of the logistic map, such as the chaotic case f(x) = 4x(1 − x), so that Ψ(x) = arcsin²(√x), hence f ⁿ(x) = sin²(2ⁿ arcsin(√x)). A nonchaotic case he also illustrated with his method, f(x) = 2x(1 − x), yielded Ψ(x) = −½ ln(1−2x), and hence f ⁿ(x) = −½((1−2x)^2ⁿ−1).

If f is the action of a group element on a set, then the iterated function corresponds to a free group.

Means of study

Iterated functions can be studied with the Artin–Mazur zeta function and with transfer operators.

In computer science

In computer science, iterated functions occur as a special case of recursive functions, which in turn anchor the study of such broad topics as lambda calculus, or narrower ones, such as the denotational semantics of computer programs.

Definitions in terms of Iterated Functions

Two important functionals can be defined in terms of iterated functions. These are Summation:

$\left\{b%2B1,\sum_{i=a}^b g(i)\right\} \equiv \left( \{i,x\} \rightarrow \{ i%2B1 ,x%2Bg(i) \}\right)^{b-a%2B1} \{a,0\}$

and the equivalent product:

$\left\{b%2B1,\prod_{i=a}^b g(i)\right\} \equiv \left( \{i,x\} \rightarrow \{ i%2B1 ,x g(i) \}\right)^{b-a%2B1} \{a,1\}$

References

^ Kuczma, Marek (1968). Functional equations in a single variable. Monografie Matematyczne. Warszawa: PWN – Polish Scientific Publishers.
^ Kuczma, M., Choczewski B., and Ger, R. (1990). Iterative Functional Equations. Cambrdige University Press. ISBN 0521355613.
^ Istratescu, Vasile (1981). Fixed Point Theory, An Introduction, D. Reidel, Holland. ISBN 90-277-1224-7.
^ Kimura, Tosihusa (1971). "On the Iteration of Analytic Functions", Funkcialaj Ekvacioj 14, 197-238.
^ Curtright, T.L.; Zachos, C.K. (2009). "Evolution Profiles and Functional Equations". Journal of Physics A 42 (48): 485208. doi:10.1088/1751-8113/42/48/485208.
^ Schröder, Ernst (1870). "Ueber iterirte Functionen". Math. Ann. 3 (2): 296–322. doi:10.1007/BF01443992.