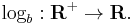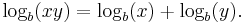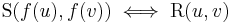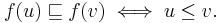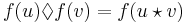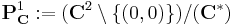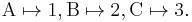Isomorphism
In abstract algebra, an isomorphism (Greek: ἴσος isos "equal", and μορφή morphe "shape") is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are structurally identical if more minute definitional differences are ignored.
More formally, an isomorphism is a bijective map f such that both f and its inverse f −1 are structure-preserving maps between two algebraic structures, that is, they are both homomorphisms.
In category theory, an isomorphism is a morphism f: X → Y in a category for which there exists an "inverse" f −1: Y → X, with the property that both f −1f = idX and f f −1 = idY.
Contents |
Purpose
Isomorphisms are studied in mathematics in order to extend insights from one phenomenon to others: if two objects are isomorphic, then any property that is preserved by an isomorphism and that is true of one of the objects, is also true of the other. If an isomorphism can be found from a relatively unknown part of mathematics into some well studied division of mathematics, where many theorems are already proved, and many methods are already available to find answers, then the function can be used to map whole problems out of unfamiliar territory over to "solid ground" where the problem is easier to understand and work with.
Practical examples
The following are examples of isomorphisms from ordinary algebra.
- Consider the logarithm function: For any fixed base b, the logarithm function logb maps from the positive real numbers R+ onto the real numbers R; formally:
- Consider the group (Z6, +), the integers from 0 to 5 with addition modulo 6. Also consider the group (Z2 × Z3, +), the ordered pairs where the x coordinates can be 0 or 1, and the y coordinates can be 0, 1, or 2, where addition in the x-coordinate is modulo 2 and addition in the y-coordinate is modulo 3. These structures are isomorphic under addition, if you identify them using the following scheme:
- (0,0) → 0
- (1,1) → 1
- (0,2) → 2
- (1,0) → 3
- (0,1) → 4
- (1,2) → 5
Abstract examples
A relation-preserving isomorphism
If one object consists of a set X with a binary relation R and the other object consists of a set Y with a binary relation S then an isomorphism from X to Y is a bijective function ƒ : X → Y such that
S is reflexive, irreflexive, symmetric, antisymmetric, asymmetric, transitive, total, trichotomous, a partial order, total order, strict weak order, total preorder (weak order), an equivalence relation, or a relation with any other special properties, if and only if R is.
For example, R is an ordering ≤ and S an ordering  , then an isomorphism from X to Y is a bijective function ƒ : X → Y such that
, then an isomorphism from X to Y is a bijective function ƒ : X → Y such that
Such an isomorphism is called an order isomorphism or (less commonly) an isotone isomorphism.
If X = Y this is a relation-preserving automorphism.
An operation-preserving isomorphism
Suppose that on these sets X and Y, there are two binary operations  and
and 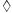 that happen to constitute the groups (X,
that happen to constitute the groups (X,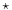 ) and (Y,
) and (Y,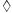 ). Note that the operators operate on elements from the domain and range, respectively, of the "one-to-one" and "onto" function ƒ. There is an isomorphism from X to Y if the bijective function ƒ : X → Y happens to produce results, that sets up a correspondence between the operator
). Note that the operators operate on elements from the domain and range, respectively, of the "one-to-one" and "onto" function ƒ. There is an isomorphism from X to Y if the bijective function ƒ : X → Y happens to produce results, that sets up a correspondence between the operator 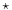 and the operator
and the operator 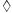 .
.
for all u, v in X.
Applications
In abstract algebra, two basic isomorphisms are defined:
- Group isomorphism, an isomorphism between groups
- Ring isomorphism, an isomorphism between rings. (Note that isomorphisms between fields are actually ring isomorphisms)
Just as the automorphisms of an algebraic structure form a group, the isomorphisms between two algebras sharing a common structure form a heap. Letting a particular isomorphism identify the two structures turns this heap into a group.
In mathematical analysis, the Laplace transform is an isomorphism mapping hard differential equations into easier algebraic equations.
In category theory, Iet the category C consist of two classes, one of objects and the other of morphisms. Then a general definition of isomorphism that covers the previous and many other cases is: an isomorphism is a morphism ƒ : a → b that has an inverse, i.e. there exists a morphism g : b → a with ƒg = 1b and gƒ = 1a. For example, a bijective linear map is an isomorphism between vector spaces, and a bijective continuous function whose inverse is also continuous is an isomorphism between topological spaces, called a homeomorphism.
In graph theory, an isomorphism between two graphs G and H is a bijective map f from the vertices of G to the vertices of H that preserves the "edge structure" in the sense that there is an edge from vertex u to vertex v in G if and only if there is an edge from ƒ(u) to ƒ(v) in H. See graph isomorphism.
In mathematical analysis, an isomorphism between two Hilbert spaces is a bijection preserving addition, scalar multiplication, and inner product.
In early theories of logical atomism, the formal relationship between facts and true propositions was theorized by Bertrand Russell and Ludwig Wittgenstein to be isomorphic. An example of this line of thinking can be found in Russell's Introduction to Mathematical Philosophy.
In cybernetics, the Good Regulator or Conant-Ashby theorem is stated "Every Good Regulator of a system must be a model of that system". Whether regulated or self-regulating an isomorphism is required between regulator part and the processing part of the system.
Relation with equality
In certain areas of mathematics, notably category theory, it is valuable to distinguish between equality on the one hand and isomorphism on the other.[1] Equality is when two objects are "literally the same", while isomorphism is when two objects "can be made to correspond via an isomorphism". For example, the sets
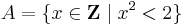 and
and 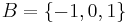
are equal – they are two different presentations (one in set builder notation, one by an enumeration) of the same subset of the integers. By contrast, the sets {A,B,C} and {1,2,3} are not equal – the first has elements that are letters, while the second has elements that are numbers. These are isomorphic as sets, since finite sets are determined up to isomorphism by their cardinality (number of elements) and these both have three elements, but there are many choices of isomorphism – one isomorphism is
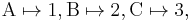 while another is
while another is 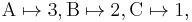
and no one isomorphism is better than any other.[note 1][note 2] Thus one cannot identify these two sets: one can choose an isomorphism between them, but any statement that identifies these two sets depends on the choice of isomorphism.
A motivating example is the distinction between a finite-dimensional vector space V and its dual space V* = { φ : V → K} of linear maps from V to its field of scalars K. These spaces have the same dimension, and thus are isomorphic as abstract vector spaces (since algebraically, vector spaces are classified by dimension, just as sets are classified by cardinality), but there is no "natural" choice of isomorphism 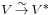 . If one chooses a basis for V, then this yields an isomorphism: For all u. v ∈ V,
. If one chooses a basis for V, then this yields an isomorphism: For all u. v ∈ V,
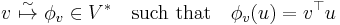 .
.
This corresponds to transforming a column vector (element of V) to a row vector (element of V*) by transpose, but a different choice of basis gives a different isomorphism: the isomorphism "depends on the choice of basis". More subtly, there is a map from a vector space V to its double dual V** = { x : V* → K} that does not depend on the choice of basis: For all v ∈ V and φ ∈ V*,
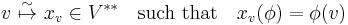 .
.
This leads to a third notion, that of a natural isomorphism: while V and V** are different sets, there is a "natural" choice of isomorphism between them. This intuitive notion of "an isomorphism that does not depend on an arbitrary choice" is formalized in the notion of a natural transformation; briefly, that one may consistently identify, or more generally map from, a vector space to its double dual, 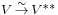 , for any vector space in a consistent way. Formalizing this intuition is a motivation for the development of category theory.
, for any vector space in a consistent way. Formalizing this intuition is a motivation for the development of category theory.
If one wishes to draw a distinction between an arbitrary isomorphism (one that depends on a choice) and a natural isomorphism (one that can be done consistently), one may write ≈ for an unnatural isomorphism and ≅ for a natural isomorphism, as in V ≈ V* and V ≅ V**. This convention is not universally followed, and authors who wish to distinguish between unnatural isomorphisms and natural isomorphisms will generally explicitly state the distinction.
Generally, saying that two objects are equal is reserved for when there is a notion of a larger (ambient) space that these objects live in. Most often, one speaks of equality of two subsets of a given set (as in the integer set example above), but not of two objects abstractly presented. For example, the 2-dimensional unit sphere in 3-dimensional space
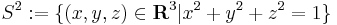 and the Riemann sphere
and the Riemann sphere 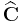
which can be presented as the one-point compactification of the complex plane C ∪ {∞} or as the complex projective line (a quotient space)
are three different descriptions for a mathematical object, all of which are isomorphic, but not equal because they are not all subsets of a single space: the first is a subset of R3, the second is C ≅ R2[note 3] plus an additional point, and the third is a subquotient of C2
See also
Notes
- ^ The careful reader may note that A, B, C have a conventional order, namely alphabetical order, and similarly 1, 2, 3 have the order from the integers, and thus in some sense there is a "natural" isomorphism, namely
- ^ In fact, there are precisely
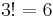 different isomorphism between two sets with three elements. This is equal to the number of automorphisms of a given three element set (which in turn is equal to the order of the symmetric group on three letters), and more generally one has that the set of isomorphisms between two objects, denoted
different isomorphism between two sets with three elements. This is equal to the number of automorphisms of a given three element set (which in turn is equal to the order of the symmetric group on three letters), and more generally one has that the set of isomorphisms between two objects, denoted 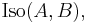 is a torsor for the automorphism group of A,
is a torsor for the automorphism group of A, 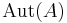 and also a torsor for the automorphism group of B. In fact, automorphisms of an object are a key reason to be concerned with the distinction between isomorphism and equality, as demonstrated in the effect of change of basis on the identification of a vector space with its dual or with its double dual, as elaborated in the sequel.
and also a torsor for the automorphism group of B. In fact, automorphisms of an object are a key reason to be concerned with the distinction between isomorphism and equality, as demonstrated in the effect of change of basis on the identification of a vector space with its dual or with its double dual, as elaborated in the sequel. - ^ Being precise, the identification of the complex numbers with the real plane,
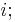 one can just as easily choose
one can just as easily choose 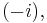 , which yields a different identification – formally, complex conjugation is an automorphism – but in practice one often assumes that one has made such an identification.
, which yields a different identification – formally, complex conjugation is an automorphism – but in practice one often assumes that one has made such an identification.
References
- ^ (Mazur 2007)
External links
- Isomorphism on PlanetMath
- Weisstein, Eric W., "Isomorphism" from MathWorld.