Isogeny

In mathematics, an isogeny is a morphism of varieties between two abelian varieties (e.g. elliptic curves) that is surjective and has a finite kernel. Every isogeny 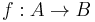$f:A\to B$ is automatically a group homomorphism between the groups of k-valued points of $A$ and $B$ , for any field k over which $f$ is defined.

1 Etymology
2 Case of elliptic curves
3 See also
4 References

Etymology

From the Greek (iso-) and Latin (genus), the term isogeny means "equal origins", a reference to the geometrical fact that an isogeny sends the point at infinity (the origin) of the source elliptic curve to the point at infinity of the target elliptic curve.

Case of elliptic curves

For elliptic curves, this notion can also be formulated as follows:

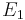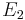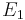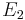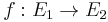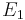Let $E_1$ and $E_2$ be elliptic curves over a field k. An isogeny between $E_1$ and $E_2$ is a surjective morphism $f: E_1\to E_2$ of varieties that preserves basepoints (i.e. $f$ maps the infinite point on $E_1$ to that on $E_2$ ).

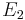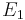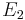Two elliptic curves $E_1$ and $E_2$ are called isogenous if there is an isogeny 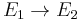$E_1\to E_2$ . This is an equivalence relation, symmetry being due to the existence of the dual isogeny. As above, every isogeny induces homomorphisms of the groups of the k-valued points of the elliptic curves.

References

Lang, Serge (1983). Abelian Varieties. Springer Verlag. ISBN 3-540-90875-7.
Mumford, David (1974). Abelian Varieties. Oxford University Press. ISBN 0-19-560528-4.

Isogeny

Contents

Etymology

Case of elliptic curves

See also

References