Isoclinism of groups
In mathematics, specifically group theory, isoclinism is an equivalence relation on groups that is broader than isomorphism, that is, any two groups that are isomorphic are isoclinic, but two isoclinic groups may not be isomorphic. The concept of isoclinism was introduced by Hall (1940) to help classify and understand p-groups, although applicable to all groups. Isoclinism remains an important part of the study of p-groups, and for instance §29 of Berkovich (2008) and §21.2 of Blackburn, Neumann & Venkataraman (2007) are devoted to it. Isoclinism also has vital consequences for the Schur multiplier and the associated aspects of character theory, as described in Suzuki (1982, p. 256) and Conway et al. (1985, Ch. 6.7).
Definition
According to Struik (1960), two groups G_1 and G_2 are isoclinic if the following three conditions hold:
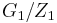 is isomorphic to
is isomorphic to 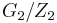 , where
, where 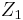 is the center of
is the center of 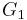 and
and 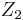 is the center of
is the center of 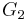 .
.- The commutator subgroup of
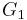 is isomorphic to the commutator subgroup of
is isomorphic to the commutator subgroup of 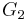 .
. - "The isomorphisms of (1) and (2) can be selected in such a way that whenever
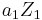 and
and 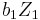 correspond respectively to
correspond respectively to 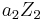 and
and 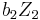 under (1), then
under (1), then 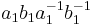 corresponds to
corresponds to 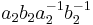 under (2)."
under (2)."
Examples
All Abelian groups are isoclinic since they are equal to their centers and their commutator subgroups are always the identity subgroup. Indeed, a group is isoclinic to an abelian group if and only if it is itself abelian, and G is isoclinic with G×A if and only if A is abelian. The dihedral, quasidihedral, and quaternion groups of order 2n are isoclinic for n≥3, Berkovich (2008, p. 285).
Isoclinism divides p-groups into families, and the smallest members of each family are called stem groups. A group is a stem group if and only if Z(G) ≤ [G,G], that is, if and only if every element of the center of the group is contained in the derived subgroup (also called the commutator subgroup), Berkovich (2008, p. 287). Some enumeration results on isoclinism families are given in Blackburn, Neumann & Venkataraman (2007, p. 226).
Another textbook treatment of isoclinism is given in Suzuki (1986, pp. 92–95), which describes in more detail the isomorphisms induced by an isoclinism. Isoclinism is important in theory of projective representations of finite groups, as all Schur covering groups of a group are isoclinic, a fact already hinted at by Hall according to Suzuki (1982, p. 256). This is important in describing the character tables of the finite simple groups, and so is described in some detail in Conway et al. (1985, Ch. 6.7).
References
- Berkovich, Yakov (2008), Groups of prime power order. Vol. 1, de Gruyter Expositions in Mathematics, 46, Walter de Gruyter GmbH & Co. KG, Berlin, doi:10.1515/9783110208221.285, ISBN 978-3-11-020418-6, MR2464640
- Blackburn, Simon R.; Neumann, Peter M.; Venkataraman, Geetha (2007), Enumeration of finite groups, Cambridge Tracts in Mathematics no 173 (1st ed.), Cambridge University Press, ISBN 978-0-521-88217-0, OCLC 154682311
- Conway, John Horton; Curtis, R. T.; Norton, S. P.; Parker, R. A.; Wilson, R. A. (1985), Atlas of finite groups, Oxford University Press, ISBN 978-0-19-853199-9, MR827219
- Hall, Philip (1940), "The classification of prime-power groups", Journal für die reine und angewandte Mathematik 182: 130–141, doi:10.1515/crll.1940.182.130, ISSN 0075-4102, MR0003389, http://resolver.sub.uni-goettingen.de/purl?GDZPPN00217491X
- Struik, Ruth Rebekka (1960), "A note on prime-power groups", Canadian Mathematical Bulletin 3: 27–30, ISSN 0008-4395, MR0148744, http://math.ca/cmb/v3/p27
- Suzuki, Michio (1982), Group theory. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 247, Berlin, New York: Springer-Verlag, ISBN 978-3-540-10915-0, MR648772
- Suzuki, Michio (1986), Group theory. II, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 248, Berlin, New York: Springer-Verlag, ISBN 978-0-387-10916-9, MR815926