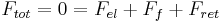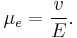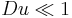Electrophoresis

For specific types of electrophoresis (for example, the process of administering medicine, iontophoresis), see Electrophoresis (disambiguation).

Electrophoresis, also called cataphoresis, is the motion of dispersed particles relative to a fluid under the influence of a spatially uniform electric field.[1][2][3][4][5][6] This electrokinetic phenomenon was observed for the first time in 1807 by Reuss (Moscow State University)[7], who noticed that the application of a constant electric field caused clay particles dispersed in water to migrate. It is ultimately caused by the presence of a charged interface between the particle surface and the surrounding fluid.

Contents

Theory

The dispersed particles have an electric surface charge, on which an external electric field exerts an electrostatic Coulomb force. According to the double layer theory, all surface charges in fluids are screened by a diffuse layer of ions, which has the same absolute charge but opposite sign with respect to that of the surface charge. The electric field also exerts a force on the ions in the diffuse layer which has direction opposite to that acting on the surface charge. This latter force is not actually applied to the particle, but to the ions in the diffuse layer located at some distance from the particle surface, and part of it is transferred all the way to the particle surface through viscous stress. This part of the force is also called electrophoretic retardation force. When the electric field is applied and the charged particle to be analyzed is at steady movement through the diffuse layer, the total resulting force is zero :

F_{tot} = 0 = F_{el} %2B F_{f} %2B F_{ret}

Considering the drag on the moving particles due to the viscosity of the dispersant, in the case of low Reynolds number and moderate electric field strength E, the velocity of a dispersed particle v is simply proportional to the applied field, which leaves the electrophoretic mobility μe defined as:

\mu_e = {v \over E}.

The most known and widely used theory of electrophoresis was developed in 1903 by Smoluchowski[8]

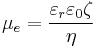\mu_e = \frac{\varepsilon_r\varepsilon_0\zeta}{\eta},

where εr is the dielectric constant of the dispersion medium, ε0 is the permittivity of free space (C² N−1 m−2), η is dynamic viscosity of the dispersion medium (Pa s), and ζ is zeta potential (i.e., the electrokinetic potential of the slipping plane in the double layer).

The Smoluchowski theory is very powerful because it works for dispersed particles of any shape at any concentration. Unfortunately, it has limitations on its validity. It follows, for instance, from the fact that it does not include Debye length κ−1. However, Debye length must be important for electrophoresis, as follows immediately from the Figure on the right. Increasing thickness of the double layer (DL) leads to removing point of retardation force further from the particle surface. The thicker DL, the smaller retardation force must be.

Detailed theoretical analysis proved that the Smoluchowski theory is valid only for sufficiently thin DL, when particle radius a is much greater than the Debye length :

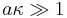a \kappa \gg 1.

This model of "thin Double Layer" offers tremendous simplifications not only for electrophoresis theory but for many other electrokinetic theories. This model is valid for most aqueous systems because the Debye length is only a few nanometers there. It breaks only for nano-colloids in solution with ionic strength close to water.

The Smoluchowski theory also neglects contribution of surface conductivity. This is expressed in modern theory as condition of small Dukhin number:

Du \ll 1

In the effort of expanding the range of validity of electrophoretic theories, the opposite asymptotic case was considered, when Debye length is larger than particle radius:

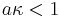a \kappa < \!\, 1.

Under this condition of a "thick Double Layer", Hückel[9] predicted the following relation for electrophoretic mobility:

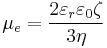\mu_e = \frac{2\varepsilon_r\varepsilon_0\zeta}{3\eta}.

This model can be useful for some nanoparticles and non-polar fluids, where Debye length is much larger than in the usual cases.

There are several analytical theories that incorporate surface conductivity and eliminate the restriction of a small Dukhin number, pioneered by Overbeek[10] and Booth.[11] Modern, rigorous theories valid for any Zeta potential and often any aκ stem mostly from Dukhin-Semenikhin theory.[12] In the thin Double Layer limit, these theories confirm the numerical solution to the problem provided by O'Brien and White.[13]

A recent set of molecular dynamics simulations have shown that even neutral particles can migrate in an electric field due to the molecular structure of water at the interface.[14]

See also

References

  1. ^ Lyklema, J. (1995). Fundamentals of Interface and Colloid Science. vol. 2. p. 3.208. 
  2. ^ Hunter, R.J. (1989). Foundations of Colloid Science. Oxford University Press. 
  3. ^ Dukhin, S.S.; B.V. Derjaguin (1974). Electrokinetic Phenomena. J. Willey and Sons. 
  4. ^ Russel, W.B.; D.A. Saville and W.R. Schowalter (1989). Colloidal Dispersions. Cambridge University Press. 
  5. ^ Kruyt, H.R. (1952). Colloid Science. Volume 1, Irreversible systems. Elsevier. 
  6. ^ Dukhin, A.S.; P.J. Goetz (2002). Ultrasound for characterizing colloids. Elsevier. 
  7. ^ Reuss, F.F. (1809). Mem. Soc. Imperiale Naturalistes de Moscow 2: 327. 
  8. ^ von Smoluchowski, M. (1903). Bull. Int. Acad. Sci. Cracovie 184. 
  9. ^ Hückel, E. (1924). Physik.Z. 25: 204. 
  10. ^ Overbeek, J.Th.G (1943). Koll.Bith: 287. 
  11. ^ Booth, F. (1948). Nature 161: 83. Bibcode 1948Natur.161...83B. doi:10.1038/161083a0. 
  12. ^ Dukhin, S.S.; N.M. Semenikhin (1970). Koll.Zhur 32: 366. 
  13. ^ O'Brien, R.W.; L.R. White (1978). J. Chem. Soc. Faraday Trans. 2 (74): 1607. 
  14. ^ Knecht et al. (2008). J. Col. Int. Sc. 318: 477. 

Further reading

External links