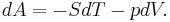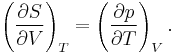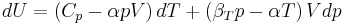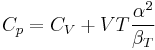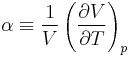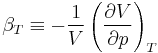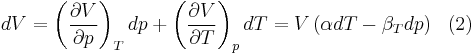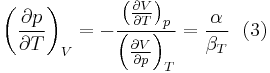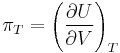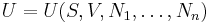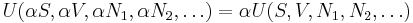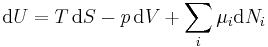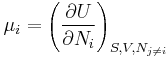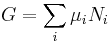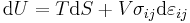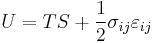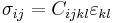Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system.[1] It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal energy has two major components, kinetic energy and potential energy. The kinetic energy is due to the motion of the system's particles (translations, rotations, vibrations), and the potential energy is associated with the static constituents of matter, static electric energy of atoms within molecules or crystals, and the static energy of chemical bonds. The internal energy of a system can be changed by heating the system or by doing work on it;[1] the first law of thermodynamics states that the increase in internal energy is equal to the total heat added and work done. If the system is isolated, its internal energy cannot change.
For practical considerations in thermodynamics or engineering it is rarely necessary, nor convenient, to consider all energies belonging to the total intrinsic energy of a sample system, such as the energy given by the equivalence of mass. Typically, descriptions only include components relevant to the system under study. Thermodynamics is chiefly concerned only with changes of the internal energy.
The internal energy is a state function of a system, because its value depends only on the current state of the system and not on the path taken or process undergone to arrive at this state. It is an extensive quantity. The SI unit of energy is the joule (J). Sometimes a corresponding intensive thermodynamic property called specific internal energy is defined, which is internal energy per a unit of mass (kilogram) of the system in question. As such, the SI unit of specific internal energy is J/kg. If intensive internal energy is expressed relative to units of amount of substance (mol), then it is referred to as molar internal energy and the unit is J/mol.
From the standpoint of statistical mechanics, the internal energy is equal to the ensemble average of the total energy of the system. It is also called intrinsic energy.
Contents |
Description and definition
The internal energy (U) is the sum of all forms of energy (Ei) intrinsic to a thermodynamic system:
It is the energy needed to create the system. It may be divided into potential energy (Upot) and kinetic energy (Ukin) components:
The kinetic energy of a system arises as the sum of the motions of all the system's particles, whether it be the motion of atoms, molecules, atomic nuclei, electrons, or other particles. The potential energy includes all energies given by the mass of particles, by the chemical composition, i.e. the chemical energy stored in chemical bonds having the potential to undergo chemical reactions, the nuclear energy stored by the configuration of protons, neutrons, and other elementary particles in atomic nuclei, and the physical force fields within the system, such as due to internal induced electric or magnetic dipole moment, as well as the energy of deformation of solids (stress-strain).
Internal energy does not include the energy due to motion of a system as a whole. It further excludes any kinetic or potential energy the body may have because of its location in external gravitational, electrostatic, or electomagnetic fields. It does, however, include the contribution to the energy due to the coupling of the internal degrees of freedom of the object to such the field. In such a case, the field is included in the thermodynamic description of the object in the form of an additional external parameter.
For practical considerations in thermodynamics or engineering, it is rarely necessary, convenient, nor even possible, to consider all energies belonging to the total intrinsic energy of a sample system, such as the energy given by the equivalence of mass. Typically, descriptions only include components relevant to the system under study. Indeed in most systems under consideration, especially through thermodynamics, it is impossible to calculate the total internal energy.[2] Therefore, a convenient null reference point may be chosen for the internal energy.
The internal energy is an extensive property: it depends on the size of the system, or on the amount of substance it contains.
At any temperature greater than absolute zero, potential energy and kinetic energy constantly converted into one another, but the sum remains constant in an isolated system (cf. table). In the classical picture of thermodynamics, kinetic energy vanishes at zero temperature and the internal energy is purely potential energy. However, quantum mechanics has demonstrated that even at zero temperature particles maintain a residual energy of motion, the zero point energy. A system at absolute zero is merely in its quantum-mechanical ground state, the lowest energy state available. At absolute zero a system has attained its minimum attainable entropy.
The kinetic energy portion of the internal energy gives rise to the temperature of the system. Statistical mechanics relates the pseudo-random kinetic energy of individual particles to the mean kinetic energy of the entire ensemble of particles comprising a system. Furthermore it relates the mean kinetic energy to the macroscopically observed empirical property that is expressed as temperature of the system. This energy is often referred to as the thermal energy of a system,[3] relating this energy, like the temperature, to the human experience of hot and cold.
Statistical mechanics considers any system to be statistically distributed across an ensemble of N microstates. Each microstate has an energy Ei and is associated with a probability pi. The internal energy is the mean value of the system's total energy, i.e., the sum of all microstate energies, each weighted by their probability of occurrence:
This is the statistical expression of the first law of thermodynamics.
Internal energy changes
|
Thermodynamics is chiefly concerned only with the changes, ΔU, in internal energy:
The most important parameters in thermodynamics when considering the changes in total energy are the changes due to the flow of heat Q and due to mechanical work, i.e. changes in volume and pressure of the system. Accordingly, the internal energy change ΔU for a process may be written more specifically as[1]
where Q is heat added to a system and Wmech is the mechanical work performed due to pressure or volume changes in the system.[note 1] All other perturbations and energies added by other processes, such as an electric current introduced into an electronic circuit, is summarized as the term Wextra.
When a system is heated, it receives energy in form of heat. This energy increases the internal energy. However, it may be extremely difficult to determine how this extra energy is stored. In general, except in an ideal gas, it is redistributed between kinetic and potential energy. The net increase in kinetic energy is measurable by an increase in the temperature of the system. The equipartition theorem states that increase in thermal energy is distributed between the available degrees of freedom of the fundamental oscillators in the system. In an ideal gas all of the extra energy results in a temperature increase, as it is stored solely as kinetic energy. The heat introduced to a system while the temperature changes is often called sensible heat.
Another method to change the internal energy of a system is by performing work on the system, either in mechanical form by changing pressure or volume, or by other perturbations, such as directing an electrical current through the system. Finally, the internal energy increases when additional mass is transferred into the system.
If a system undergoes certain phase transformations while being heated, such as melting and vaporization, it may be observed that the temperature of the system does not change until the entire sample has completed the transformation. The energy introduced into the system while the temperature did not change is called a latent energy, or latent heat, in contrast to sensible heat. It increases only the potential energy of the system, but not its thermal energy component.
Internal energy of the ideal gas
Thermodynamics often uses the concept of the ideal gas for teaching purposes, and as an approximation for working systems. The ideal gas is a gas of particles considered as point objects of perfect spherical symmetry that interact only by elastic collisions and fill a volume such that their free mean path between collisions is much larger than their diameter. Such systems are approximated by the monoatomic gases, helium and the other noble gases. Here the kinetic energy consists only of the translational energy of the individual atoms. Monoatomic particles are not considered to rotate or vibrate, and are not electronically excited to higher energies except at very high temperatures.
Therefore practical internal energy changes in an ideal gas may be described solely by changes in its kinetic energy.
Internal energy of a closed thermodynamic system
This above summation of all components of change in internal energy assume that a positive energy denotes heat added to the system or work done on the system, while a negative energy denotes work of the system on the environment.
Typically this relationship is expressed in infinitesimal terms using the differentials of each term. Only the internal energy is an exact differential. For a system undergoing only thermodynamics processes, i.e. a closed system that can exchange only heat and work, the change in the internal energy is
which constitutes the first law of thermodynamics.[note 1] It may be expressed in terms of other thermodynamic parameters. Each term is composed of an intensive variable (a generalized force) and its conjugate infinitesimal extensive variable (a generalized displacement).
For example, for a non-viscous fluid, the mechanical work done on the system may be related to the pressure p and volume V. The pressure is the intensive generalized force, while the volume is the extensive generalized displacement:
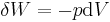 .
.
This defines the direction of work, W, to be energy flow from the working system to the surroundings, indicated by a negative term.[note 1] Taking the direction of heat transfer Q to be into the working fluid and assuming a reversible process, the heat is
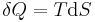 .
.
 is temperature
is temperature is entropy
is entropy
and the change in internal energy becomes
Changes due to temperature and volume
The expression relating changes in internal energy to changes in temperature and volume is
This is useful if the equation of state is known.
In case of an ideal gas, we can derive that 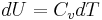 , i.e. the internal energy of an ideal gas can be written as a function that depends only on the temperature.
, i.e. the internal energy of an ideal gas can be written as a function that depends only on the temperature.
The expression relating changes in internal energy to changes in temperature and volume is
The equation of state is the ideal gas law
Solve for pressure:
Substitute in to internal energy expression:
Take the derivative of pressure with respect to temperature:
Replace:
And simplify:
To express dU in terms of dT and dV, the term
is substituted in the fundamental thermodynamic relation
This gives:
The term 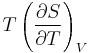 is the heat capacity at constant volume
is the heat capacity at constant volume 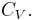
The partial derivative of S with respect to V can be evaluated if the equation of state is known. From the fundamental thermodynamic relation, it follows that the differential of the Helmholtz free energy A is given by:
The symmetry of second derivatives of A with respect to T and V yields the Maxwell relation:
This gives the expression above.
Changes due to temperature and pressure
When dealing with fluids or solids, an expression in terms of the temperature and pressure is usually more useful:
where it is assumed that the heat capacity at constant pressure is related to the heat capacity at constant volume according to:
The partial derivative of the pressure with respect to temperature at constant volume can be expressed in terms of the coefficient of thermal expansion
and the isothermal compressibility
by writing:
and equating dV to zero and solving for the ratio dp/dT. This gives:
Substituting (2) and (3) in (1) gives the above expression.
Changes due to volume at constant pressure
The internal pressure is defined as a partial derivative of the internal energy with respect to the volume at constant temperature:
Internal energy of multi-component systems
In addition to including the entropy S and volume V terms in the internal energy, a system is often described also in terms of the number of particles or chemical species it contains:
where the terms Nj are the numbers of constituents of type j in the system. The internal energy is an extensive function of the extensive variables variables S, V, and the set of components 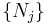 , the internal energy may be written as a linear homogeneous function of first degree:
, the internal energy may be written as a linear homogeneous function of first degree:
where α is a factor describing the growth of the system. The differential internal energy may be written as
where the coefficients 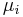 are the chemical potentials for the components of type i in the system. The chemical potentials are defined as the partial derivatives of the energy with respect to the variations in composition:
are the chemical potentials for the components of type i in the system. The chemical potentials are defined as the partial derivatives of the energy with respect to the variations in composition:
As conjugate variables to the composition 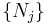 , the chemical potentials are intensive properties, intrinsically characteristic of the system, and not dependent on its extent. Because of the extensive nature of U and its variables, the differential dU may be integrated and yields an expression for the internal energy:
, the chemical potentials are intensive properties, intrinsically characteristic of the system, and not dependent on its extent. Because of the extensive nature of U and its variables, the differential dU may be integrated and yields an expression for the internal energy:
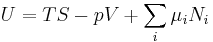 .
.
The sum over the composition of the system is the Gibbs energy:
that arises from changing the composition of the system at constant temperature and pressure. For a single component system, the chemical potential equals the Gibbs energy per amount of substance, i.e. particles or moles according to the original definition of the unit for 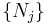 .
.
Internal energy in an elastic medium
For an elastic medium the mechanical energy term of the internal energy must be replaced by the more general expression involving the stress 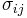 and strain
and strain 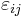 . The infinitesimal statement is:
. The infinitesimal statement is:
where Einstein notation has been used for the tensors, in which there is a summation over all repeated indices in the product term. The Euler theorem yields for the internal energy:[4]
For a linearly elastic material, the stress can be related to the strain by:
Where Cijkl is an element of the 4th-rank elastic constant tensor of the medium.
Computational methods
The path integral Monte Carlo method is a numerical approach for determining the values of the internal energy, based on quantum dynamical principles.
History
James Joule studied the relationship between heat, work, and temperature. He observed that if he did mechanical work on a fluid, such as water, by agitating the fluid, its temperature increased. He proposed that the mechanical work he was doing on the system was converted to thermal energy. Specifically, he found that 4185.5 joules of energy were needed to raise the temperature of a kilogram of water by one degree Celsius.
Notes
- ^ a b c In this article we choose the sign convention of the mechanical work as typically defined in chemistry, which is different from the convention used in physics. In chemistry, work performed by the system against the environment, e.g., a system expansion, is negative, while in physics this is taken to be positive.
See also
- Calorimetry
- Enthalpy
- Gibbs free energy
- Helmholtz free energy
- Thermodynamic equations
- Thermodynamic potentials
References
- ^ a b c Peter Atkins, Julio de Paula (2006). Physical Chemistry (8 ed.). Oxford University Press. p. 9.
- ^ I. Klotz, R. Rosenberg, Chemical Thermodynamics - Basic Concepts and Methods, 7th ed., Wiley (2008), p.39
- ^ Thermal energy – Hyperphysics
- ^ Landau & Lifshitz 1986
Bibliography
- Alberty, R. A. (2001). "Use of Legendre transforms in chemical thermodynamics" (PDF). Pure Appl. Chem. 73 (8): 1349–1380. doi:10.1351/pac200173081349. http://www.iupac.org/publications/pac/2001/pdf/7308x1349.pdf.
- Lewis, Gilbert Newton; Randall, Merle: Revised by Pitzer, Kenneth S. & Brewer, Leo (1961). Thermodynamics (2nd ed.). New York, NY USA: McGraw-Hill Book Co.. ISBN 0-07-113809-9.
- Landau, L. D.; Lifshitz, E. M. (1986). Theory of Elasticity (Course of Theoretical Physics Volume 7). (Translated from Russian by J.B. Sykes and W.H. Reid) (Third ed.). Boston, MA: Butterworth Heinemann. ISBN 0-7506-2633-X.
|
||||||||||||||

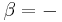
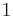
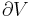

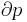
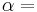
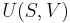


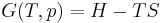
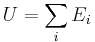
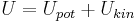
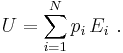
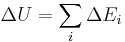
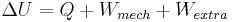
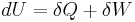
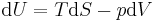
![dU =C_{V}dT %2B\left[T\left(\frac{\partial p}{\partial T}\right)_{V} - p\right]dV\,\,\text{ (1)}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/8c08c1d4217d2673d51051fad0787989.png)
![dU =C_{V}dT %2B\left[T\left(\frac{\partial p}{\partial T}\right)_{V} - p\right]dV.\,](/2012-wikipedia_en_all_nopic_01_2012/I/46a486fe3d368ef3b3931122a4786b20.png)
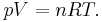
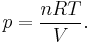
![dU =C_{V}dT %2B\left[T\left(\frac{\partial p}{\partial T}\right)_{V} - \frac{n R T}{V}\right]dV.\,](/2012-wikipedia_en_all_nopic_01_2012/I/b8d1286ec91f6787c358b1125b9bfb52.png)
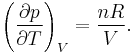
![dU = C_{V}dT %2B \left[ \frac{n R T}{V} - \frac{n R T}{V} \right] dV.](/2012-wikipedia_en_all_nopic_01_2012/I/23bb88949d3f2d53bb4b767d8164b540.png)
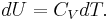
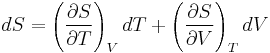
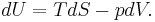
![dU = T\left(\frac{\partial S}{\partial T}\right)_{V}dT %2B\left[T\left(\frac{\partial S}{\partial V}\right)_{T} - p\right]dV.\,](/2012-wikipedia_en_all_nopic_01_2012/I/c5c8591cbfc40651bcfb2f9bc72d66a1.png)