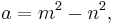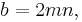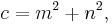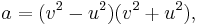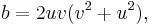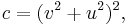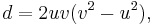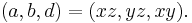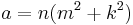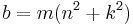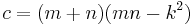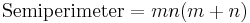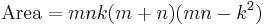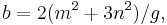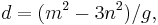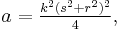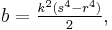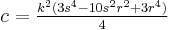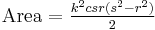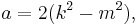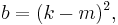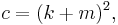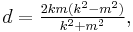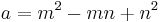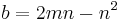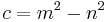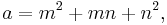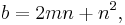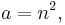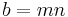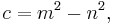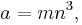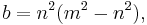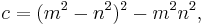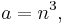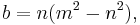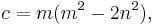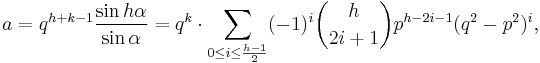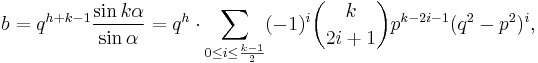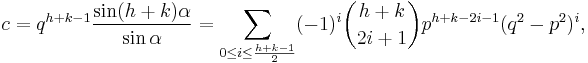Integer triangle
An integer triangle or integral triangle is a triangle all of whose sides have lengths that are integers. A rational triangle can be defined as one having all sides with rational length; any such rational triangle can be integrally rescaled (can have all sides multiplied by the same integer, namely a common multiple of their denominators) to obtain an integer triangle, so there is no substantive difference between integer triangles and rational triangles in this sense. (Note however, that other definitions of the term "rational triangle" also exist: In 1914 Carmichael[1] used the term in the sense that we today use the term Heronian triangle; Somos[2] uses it to refer to triangles whose ratios of sides are rational; Conway and Guy [3] define a rational triangle as one with rational sides and rational angles measured in degrees—in which case the only rational triangle is the equilateral triangle.)
Pythagorean triangles
A Pythagorean triangle has a right angle and three integer sides, which are known as a Pythagorean triple or Pythagorean triplet or Pythagorean triad.[4] All Pythagorean triples 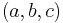 with hypotenuse
with hypotenuse  which are primitive (the sides having no common factor) can be generated by
which are primitive (the sides having no common factor) can be generated by
where m and n are coprime integers and one of them is even with m > n.
Pythagorean triangles with integer altitude from the hypotenuse
All primitive Pythagorean triangles with legs a b, hypotenuse c, and integer altitude  from the hypotenuse, which necessarily have both
from the hypotenuse, which necessarily have both 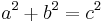 and
and 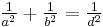 , are generated by[5][6]
, are generated by[5][6]
for coprime integers u, v with v > u.
Furthermore, any Pythagorean triangle with legs x, y and hypotenuse z can generate another Pythagorean triangle, this one with integer altitude d from the hypotenuse c, by[6]
Heronian triangles
A Heronian triangle, also known as a Heron triangle or a Hero triangle, is a triangle with integer sides and integer area. All Heronian triangles can be generated[7] as multiples of
for integers m, n and k subject to the contraints:
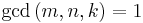
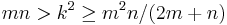
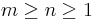 .
.
Heronian triangles with sides in arithmetic progression
A triangle with integer sides and integer area has sides in arithmetic progression if and only if[8] the sides are (b – d, b, b + d), where
and where g is the greatest common divisor of 
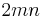 , and
, and 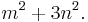
Heronian triangles with one angle equal to twice another
All Heronian triangles with B=2A are generated by[9] either
with integers k, s, r such that s2 > 3r2, or
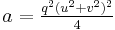 ,
,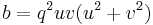 ,
,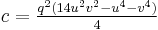 ,
,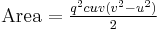 ,
,
with integers q, u, v such that v > u and v2 < (7+4√3)u2.
No triangles with B = 2A are Pythagorean.
Other integer triangles
Integer triangles with a rational angle bisector
A triangle family with integer sides 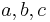 and with rational bisector
and with rational bisector  of angle A is given by[10]
of angle A is given by[10]
with integers 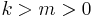 .
.
Integer triangles with a 60° angle
Integer triangles with a 60° angle can be generated by[11]
with coprime integers m, n with 0 < n < m (the angle of 60° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. an equilateral triangle solution is obtained by taking m = 2 and n = 1, but this produces a = b = c = 3, which is not a primitive solution). See also [12][13]
Integer triangles with a 120° angle
Integer triangles with a 120° angle can be generated by[14]
with coprime integers m, n with 0 < n < m (the angle of 120° is opposite to the side of length a). From here, all primitive solutions can be obtained by dividing a, b, and c by their greatest common divisor (e.g. by taking m = 4 and n = 1, one obtains a = 21, b = 9 and c = 15, which is not a primitive solution, but leads to the primitive solution a = 7, b = 3, and c = 5 which, up to order, can be obtained with the values m = 2 and n = 1). See also.[12][13]
Integer triangles with one angle equal to twice another
With angle A opposite side  and angle B opposite side
and angle B opposite side  , some triangles with B=2A are generated by[15]
, some triangles with B=2A are generated by[15]
with integers m, n such that 0 < n < m < 2n.
Note that all triangles with B = 2A (whether integer or not) have[16] 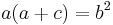 .
.
Integer triangles with one angle equal to 3/2 times another
The equivalence class of similar triangles with 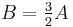 are generated by[15]
are generated by[15]
with integers 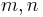 such that
such that 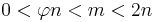 , where
, where 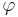 is the golden ratio
is the golden ratio 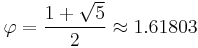 .
.
Note that all triangles with 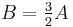 (whether with integer sides or not) satisfy
(whether with integer sides or not) satisfy 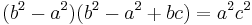 .
.
Integer triangles with one angle three times another
We can generate the full equivalence class of similar triangles that satisfy B=3A by using the formulas [17]
where  and
and  are integers such that
are integers such that 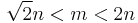 .
.
Note that all triangles with B = 3A (whether with integer sides or not) satisfy 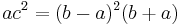 .
.
Integer triangles with one angle equal to an arbitrary rational number times another angle
For positive relatively prime integers h and k, the triangle with the following sides has angles 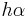 ,
, 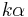 , and
, and 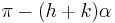 and hence two angles in the ratio h : k, and its sides are integers:[18]
and hence two angles in the ratio h : k, and its sides are integers:[18]
where 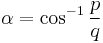 and p and q are any relatively prime integers such that
and p and q are any relatively prime integers such that 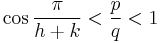 .
.
Properties
- The only triangle with consecutive integers for sides and area has sides
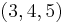 and area
and area 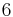 .
.
- The only triangle with consecutive integers for an altitude and the sides has sides
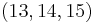 and altitude from side 14 equal to 12.
and altitude from side 14 equal to 12.
- The
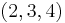 triangle and its multiples are the only triangles with integer sides in arithmetic progression and having the complementary exterior angle property.[19][20][21] This property states that if angle C is obtuse and if a segment is dropped from B meeting perpendicularly AC extended at P, then ∠CAB=2∠CBP.
triangle and its multiples are the only triangles with integer sides in arithmetic progression and having the complementary exterior angle property.[19][20][21] This property states that if angle C is obtuse and if a segment is dropped from B meeting perpendicularly AC extended at P, then ∠CAB=2∠CBP.
- The
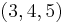 triangle and its multiples are the only integer right triangles having sides in arithmetic progression[21]
triangle and its multiples are the only integer right triangles having sides in arithmetic progression[21]
- The
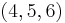 triangle and its multiples are the only triangles with one angle being twice another and having integer sides in arithmetic progression.[21]
triangle and its multiples are the only triangles with one angle being twice another and having integer sides in arithmetic progression.[21]
- The
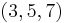 triangle and its multiples are the only triangles with a 120° angle and having integer sides in arithmetic progression.[21]
triangle and its multiples are the only triangles with a 120° angle and having integer sides in arithmetic progression.[21]
- The only integer triangle with area=semiperimeter[22] has sides
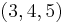 .
.
- The only integer triangles with area = perimeter have sides[22][23] (5, 12, 13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17). Of these the first two, but not the last three, are right triangles.
- The perimeter of a Heron triangle is always an even number.[24]
- The area of a Heron triangle is always divisible by 6.[24]
- There are no equilateral Heronian triangles.
- There are no Heronian triangles whose side lengths form a geometric progression.[8]
- There exist integer triangles with three rational medians.[4]:p. 64 The smallest has sides (68, 85, 87). Others include (127, 131, 158) and (204, 255, 261).
References
- ^ Carmichael, R. D., 1914, Diophantine Analysis, pp.11-13; in R. D. Carmichael, 1959, The Theory of Numbers and Diophantine Analysis, Dover.
- ^ Somos, M., "Rational triangles," http://grail.csuohio.edu/~somos/rattri.html
- ^ Conway, J. H., and Guy, R. K., "The only rational triangle," in The Book of Numbers, 1996, Springer-Verlag, pp.201 and 228-239.
- ^ a b Sierpiński, Wacław. Pythagorean Triangles, Dover Publ., 2003 (orig. 1962).
- ^ Voles, Roger, "Integer solutions of
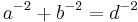 ," Mathematical Gazette 83, July 1999, 269–271.
," Mathematical Gazette 83, July 1999, 269–271. - ^ a b Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
- ^ Carmichael, R. D. The Theory of Numbers and Diophantine Analysis. New York: Dover, 1952.
- ^ a b Buchholz, R. H.; MacDougall, J. A.. "Heron Quadrilaterals with sides in Arithmetic or Geometric progression". Bull. Austral. Math. Soc. pp:263-269; Vol. 59 (1999). http://journals.cambridge.org/article_S0004972700032883.
- ^ Mitchell, Douglas W., "Heron triangles with ∠B=2∠A," Mathematical Gazette 91, July 2007, 326–328.
- ^ Zelator, Konstantine, Mathematical Spectrum 39(3), 2006/2007, 59-62.
- ^ Gilder, J., Integer-sided triangles with an angle of 60°," Mathematical Gazette 66, December 1982, 261 266
- ^ a b Burn, Bob, "Triangles with a 60° angle and sides of integer length," Mathematical Gazette 87, March 2003, 148–153.
- ^ a b Read, Emrys, "On integer-sided triangles containing angles of 120° or 60°", Mathematical Gazette 90, July 2006, 299-305.
- ^ Selkirk, K., "Integer-sided triangles with an angle of 120°," Mathematical Gazette 67, December 1983, 251–255.
- ^ a b Deshpande,M. N., "Some new triples of integers and associated triangles," Mathematical Gazette 86, November 2002, 464–466.
- ^ Willson, William Wynne, "A generalisation of the property of the 4, 5, 6 triangle," Mathematical Gazette 60, June 1976, 130–131.
- ^ Parris, Richard, College Mathematics Journal 38(5), November 2007, 345-355.
- ^ Hirschhorn, Michael D., "Commensurable triangles", Mathematical Gazette 95, March 2011, pp. 61-63.
- ^ Barnard, T., and Silvester, J., "Circle theorems and a property of the (2,3,4) triangle," Mathematical Gazette 85, July 2001, 312-316.
- ^ Lord, N., "A striking property of the (2,3,4) triangle," Mathematical Gazette 82, March 1998, 93-94.
- ^ a b c d Mitchell, Douglas W., "The 2:3:4, 3:4:5, 4:5:6, and 3:5:7 triangles," Mathematical Gazette 92, July 2008.
- ^ a b MacHale, D., "That 3,4,5 triangle again," Mathematical Gazette 73, March 1989, 14-16.
- ^ Dickson, History of the Theory of Numbers, vol.2, 181.
- ^ a b Friche, Jan. "On Heron Simplices and Integer Embedding". Ernst-Moritz-Arndt Universät Greiswald Publication, 2 Jan. 2002. http://www.math-inf.uni-greifswald.de/~fricke/publikationen/heron.pdf.