Information geometry

Information geometry is a branch of mathematics that applies the techniques of differential geometry to the field of probability theory. It derives its name from the fact that the Fisher information is used as the Riemannian metric when considering the geometry of probability distribution families that form a Riemannian manifold. Notably, information geometry has been used to prove the higher-order efficiency properties of the maximum-likelihood estimator.

Information geometry reached maturity through the work of Shun'ichi Amari and other Japanese mathematicians in the 1980s. Amari and Nagaoka's book, Methods of Information Geometry^[1], is currently the de facto reference book of the relatively young field due to its broad coverage of significant developments attained using the methods of information geometry up to the year 2000. Many of these developments were previously only available in Japanese-language publications.

1 Introduction
2 Examples
3 Fisher information metric as a Riemannian metric
4 History
5 Some applications
- 5.1 Natural gradient
- 5.2 Nonlinear filtering
6 See also
7 References
8 External links

Introduction

In information geometry, a family (similar collection) of probability distributions over the random variable (or vector), X, is viewed as forming a manifold, M, with coordinate system, $\Xi =\{\xi | \xi \in \real^n \}$ . One possible coordinate system for the manifold is the free parameters of the probability distribution family. Each point, P, in the manifold, M, with coordinate $\xi$ , carries a function on the random variable (or vector), i.e. the probability distribution. We write this as $P = p(x; \xi)$ . The set of all points, P, in the probability family forms the manifold, M.

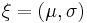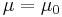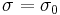For example, with the family of normal distributions, the ordered pair of the mean, $\mu$ , and standard deviation, $\sigma$ , form one possible coordinate system, $\xi = (\mu, \sigma)$ . Each particular point in the manifold, such as $\mu=\mu_0$ and $\sigma = \sigma_0$ , carries a specific normal distribution with mean, 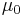$\mu_0$ , and standard deviation, 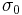$\sigma_0$ , so that

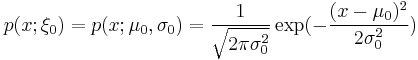$p(x;\xi_0)=p(x; \mu_0, \sigma_0)= \frac{1}{\sqrt{2\pi\sigma_0^2}} \exp( -\frac{(x-\mu_0)^2}{2\sigma_0^2} )$ .

To form a Riemannian manifold on which the techniques of differential geometry can be applied, a Riemannian metric must be defined. Information geometry takes the Fisher information to be the "natural" metric, although it is not the only possible metric. The Fisher information is re-termed to be called the "Fisher metric" and, significantly, is invariant under coordinate transformation.

Examples

The main tenet of information geometry is that many important structures in probability theory, information theory and statistics can be treated as structures in differential geometry by regarding a space of probability distributions as a differentiable manifold endowed with a Riemannian metric and a family of affine connections distinct from the canonical affine connection. The e-affine connection and m-affine connection geometrize expectation and maximization, as in the expectation-maximization algorithm.

For example,

The Fisher information metric is a Riemannian metric.^[1]
The Kullback-Leibler divergence is one of a family of divergences related to dual affine connections.^[1]
An exponential family is flat submanifold under the e-affine connection.^[1]
The maximum likelihood estimate may be obtained through projection onto the chosen statistical model using the m-affine connection.^[2]^[1]
The unique existence of maximum likelihood estimate on exponential families is the consequence of the e- and m- connections being dual affine.
The em-algorithm, (em here stands for: e-projection, m-projection) which behaves similarly to the canonical EM algorithm for most cases is, under broad conditions, an iterative dual projection method via the e-connection and m-connection.^[3]
The concepts of accuracy of estimators, in particular the first and third order efficiency of estimators, can be represented in terms of imbedding curvatures of the manifold representing the statistical model and the manifold of representing the estimator (the second order always equals zero after bias correction).
The higher order asymptotic power of statistical test can be represented using geometric quantities.

The importance of studying statistical structures as geometrical structures lies in the fact that geometric structures are invariant under coordinate transforms. For example, the Fisher information metric is invariant under coordinate transformation.^[1]

The statistician Fisher recognized in the 1920s that there is an intrinsic measure of amount of information for statistical estimators. The Fisher information matrix was shown by Cramer and Rao to be a Riemannian metric on the space of probabilities, and became known as Fisher information metric.

The mathematician Cencov (Chentsov) proved in the 1960s and 1970s that on the space of probability distributions on a sample space containing at least three points,

There exists a unique intrinsic metric. It is the Fisher information metric.
There exists a unique one parameter family of affine connections. It is the family of $\alpha$ -affine connections later popularized by Amari.

Both of these uniqueness are, of course, up to the multiplication by a constant.

Amari and Nagaoka's study in the 1980s brought all these results together, with the introduction of the concept of dual-affine connections, and the interplay among metric, affine connection and divergence. In particular,

Given a Riemannian metric g and a family of dual affine connections 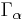$\Gamma_\alpha$ , there exists a unique set of dual divergences 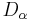$D_\alpha$ defined by them.
Given the family of dual divergences 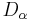$D_\alpha$ , the metric and affine connections can be uniquely determined by second order and third order differentiations.

Also, Amari and Kumon showed that asymptotic efficiency of estimates and tests can be represented by geometrical quantities.

Fisher information metric as a Riemannian metric

Main article: Fisher information metric

Information geometry makes frequent use of the Fisher information metric:

$g_{jk}(\xi)=\int \frac{\partial \log p(x;\xi)}{\partial \xi_j} \frac{\partial \log p(x;\xi)}{\partial \xi_k} p(x;\xi)\, dx.$

Substituting 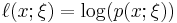$\ell(x;\xi) = \log(p(x; \xi))$ from information theory, the formula becomes:

$g_{jk}(\xi)=\int \frac{\partial \ell(x,\xi)}{\partial \xi_j} \frac{\partial \ell(x,\xi)}{\partial \xi_k} p(x,\xi)\, dx.$

History

The history of information geometry is associated with the discoveries of at least the following people, and many others

Some applications

Natural gradient

An important concept on information geometry is the natural gradient. The concept and theory of the natural gradient suggests an adjustment to the energy function of a learning rule. This adjustment takes into account the curvature of the (prior) statistical differential manifold, by way of the Fisher information metric.

This concept has many important applications in blind signal separation, neural networks, artificial intelligence, and other engineering problems that deal with information. Experimental results have shown that application of the concept leads to substantial performance gains.

Nonlinear filtering

Other applications concern statistics of stochastic processes and approximate finite dimensional solutions of the filtering problem (stochastic processes). As the nonlinear filtering problem admits an infinite dimensional solution in general, one can use a geometric structure in the space of probability distributions to project the infinite dimensional filter into an approximate finite dimensional one, leading to the projection filters introduced in 1987 by Bernard Hanzon.

References

^ ^a ^b ^c ^d ^e ^f Shun'ichi Amari, Hiroshi Nagaoka - Methods of information geometry, Translations of mathematical monographs; v. 191, American Mathematical Society, 2000 (ISBN 978-0821805312)
^ Shun'ichi Amari - Differential-geometrical methods in statistics, Lecture notes in statistics, Springer-Verlag, Berlin, 1985.
^ S. Amari, Information geometry of the EM and em algorithms for neural networks, Neural Networks, vol. 8, 1995, pp. 1379-1408.

M. Murray and J. Rice - Differential geometry and statistics, Monographs on Statistics and Applied Probability 48, Chapman and Hall, 1993.
R. E. Kass and P. W. Vos - Geometrical Foundations of Asymptotic Inference, Series in Probability and Statistics, Wiley, 1997.
N. N. Cencov - Statistical Decision Rules and Optimal Inference, Translations of Mathematical Monographs; v. 53, American Mathematical Society, 1982
Giovanni Pistone, and Sempi, C. (1995). An infinitedimensional geometric structure on the space of all the probability measures equivalent to a given one, Ann. Statist. 23, no. 5, 1543–1561.
Brigo, D, Hanzon, B, Le Gland, F, Approximate nonlinear filtering by projection on exponential manifolds of densities, BERNOULLI, 1999, Vol: 5, Pages: 495 - 534, ISSN: 1350-7265
Brigo, D, Diffusion Processes, Manifolds of Exponential Densities, and Nonlinear Filtering, In: Ole E. Barndorff-Nielsen and Eva B. Vedel Jensen, editor, Geometry in Present Day Science, World Scientific, 1999
Arwini, Khadiga, Dodson, C. T. J. Information Geometry - Near Randomness and Near Independence, Lecture Notes in Mathematics Vol. 1953, Springer 2008

External links

Manifold Learning and its Applications AAAI 2010
Information Geometry overview by Cosma Rohilla Shalizi, July 2010
blog Computational Information Geometry Wonderland by Frank Nielsen