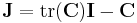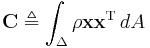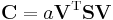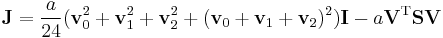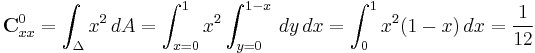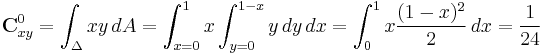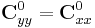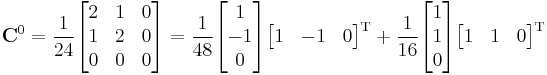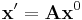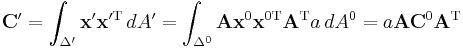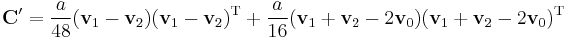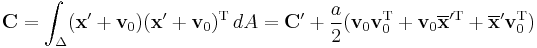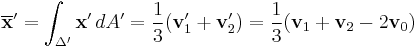Inertia tensor of triangle
The inertia tensor  of a triangle (like the inertia tensor of any body) can be expressed in terms of covariance
of a triangle (like the inertia tensor of any body) can be expressed in terms of covariance 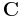 of the body:
of the body:
where covariance is defined as area integral over the triangle:
Covariance for a triangle in three-dimensional space, assuming that mass is equally distributed over the surface with unit density, is
where
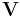 represents 3 × 3 matrix containing triangle vertex coordinates
represents 3 × 3 matrix containing triangle vertex coordinates 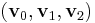 in the rows,
in the rows,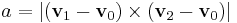 is twice the area of the triangle,
is twice the area of the triangle,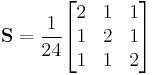
Substitution of triangle covariance in definition of inertia tensor gives eventually
Contents |
A proof of the formula
The proof given here follows the steps from the article.[1]
Covariance of a canonical triangle
Let's compute covariance of the right triangle with the vertices (0,0,0), (1,0,0), (0,1,0).
Following the definition of covariance we receive
The rest components of 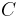 are zero because the triangle is in
are zero because the triangle is in 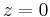 .
.
As a result
Covariance of the triangle with a vertex in the origin
Consider a linear operator
that maps the canonical triangle in the triangle 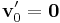 ,
, 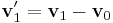 ,
, 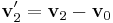 . The first two columns of
. The first two columns of 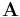 contain
contain 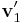 and
and 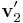 respectively, while the third column is arbitrary. The target triangle is equal to the triangle in question (in particular their areas are equal), but shifted with its zero vertex in the origin.
respectively, while the third column is arbitrary. The target triangle is equal to the triangle in question (in particular their areas are equal), but shifted with its zero vertex in the origin.
Covariance of the triangle in question
The last thing remaining to be done is to conceive how covariance is changed with the translation of all points on vector 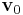 .
.
where
is the centroid of dashed triangle.
It's easy to check now that all coefficients in 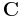 before
before 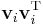 is
is 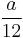 and before
and before 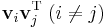 is
is 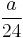 . This can be expressed in matrix form with
. This can be expressed in matrix form with 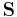 as above.
as above.
References
- ^ http://number-none.com/blow/inertia/bb_inertia.doc Jonathan Blow, Atman J Binstock (2004) "How to find the inertia tensor (or other mass properties) of a 3D solid body represented by a triangle mesh"