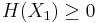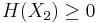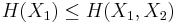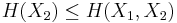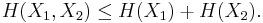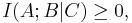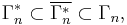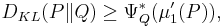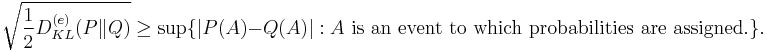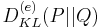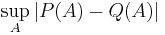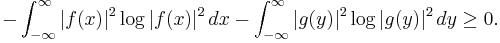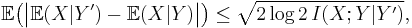Inequalities in information theory

Inequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.

1 Shannon-type inequalities
2 Non-Shannon-type inequalities
3 Lower bounds for the Kullback–Leibler divergence
4 Other inequalities
- 4.1 Hirschman uncertainty
- 4.2 Tao's inequality
5 See also
6 References
7 External links

Shannon-type inequalities

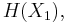
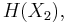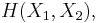Consider a finite collection of finitely (or at most countably) supported random variables on the same probability space. For a collection of n random variables, there are 2ⁿ − 1 such non-empty subsets for which entropies can be defined. For example, when n = 2, we may consider the entropies $H(X_1),$ $H(X_2),$ and $H(X_1, X_2),$ and express the following inequalities (which together characterize the range of the marginal and joint entropies of two random variables):

$H(X_1) \ge 0$
$H(X_2) \ge 0$
$H(X_1) \le H(X_1, X_2)$
$H(X_2) \le H(X_1, X_2)$
$H(X_1, X_2) \le H(X_1) %2B H(X_2).$

In fact, these can all be expressed as special cases of a single inequality involving the conditional mutual information, namely

$I(A;B|C) \ge 0,$

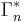where $A$ , $B$ , and $C$ each denote the joint distribution of some arbitrary (possibly empty) subset of our collection of random variables. Inequalities that can be derived from this are known as Shannon-type inequalities. More formally, (following the notation of Yeung), define $\Gamma^*_n$ to be the set of all constructible points in 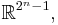$\mathbb R^{2^n-1},$ where a point is said to be constructible if and only if there is a joint, discrete distribution of n random variables such that each coordinate of that point, indexed by a non-empty subset of {1, 2, ..., n}, is equal to the joint entropy of the corresponding subset of the n random variables. The closure of 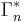$\Gamma^*_n$ is denoted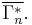 $\overline{\Gamma^*_n}.$

The cone in 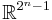$\mathbb R^{2^n-1}$ characterized by all Shannon-type inequalities among n random variables is denoted 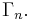$\Gamma_n.$ Software has been developed to automate the task of proving such inequalities.^[1]^[2] Given an inequality, such software is able to determine whether the given inequality contains the cone 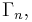$\Gamma_n,$ in which case the inequality can be verified, since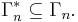 $\Gamma^*_n \subseteq \Gamma_n.$

Non-Shannon-type inequalities

Other, less trivial inequalities have been discovered among the entropies and joint entropies of four or more random variables, which cannot be derived from Shannon's basic inequalities.^[3]^[4] These are known as non-Shannon-type inequalities.

It was shown that

$\Gamma^*_n \subset \overline{\Gamma^*_n} \subset \Gamma_n,$

where the inclusions are proper for 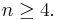$n \ge 4.$ All three of these sets are, in fact, convex cones.

Lower bounds for the Kullback–Leibler divergence

A great many important inequalities in information theory are actually lower bounds for the Kullback–Leibler divergence. Even the Shannon-type inequalities can be considered part of this category, since the bivariate mutual information can be expressed as the Kullback–Leibler divergence of the joint distribution with respect to the product of the marginals, and thus these inequalities can be seen as a special case of Gibbs' inequality.

On the other hand, it seems to be much more difficult to derive useful upper bounds for the Kullback–Leibler divergence. This is because the Kullback–Leibler divergence D_KL(P||Q) depends very sensitively on events that are very rare in the reference distribution Q. D_KL(P||Q) increases without bound as an event of finite non-zero probability in the distribution P becomes exceedingly rare in the reference distribution Q, and in fact D_KL(P||Q) is not even defined if an event of non-zero probability in P has zero probability in Q. (Hence the requirement that P be absolutely continuous with respect to Q.)

Gibbs' inequality

Main article: Gibbs' inequality

This fundamental inequality states that the Kullback–Leibler divergence is non-negative.

Kullback's inequality

Main article: Kullback's inequality

Another inequality concerning the Kullback–Leibler divergence is known as Kullback's inequality.^[5] If P and Q are probability distributions on the real line with P absolutely continuous with respect to Q, and whose first moments exist, then

$D_{KL}(P\|Q) \ge \Psi_Q^*(\mu'_1(P)),$

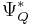where $\Psi_Q^*$ is the large deviations rate function, i.e. the convex conjugate of the cumulant-generating function, of Q, and 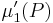$\mu'_1(P)$ is the first moment of P.

The Cramér–Rao bound is a corollary of this result.

Pinsker's inequality

Main article: Pinsker's inequality

Pinsker's inequality relates Kullback–Leibler divergence and total variation distance. It states that if P, Q are two probability distributions, then

$\sqrt{\frac{1}{2}D_{KL}^{(e)}(P\|Q)} \ge \sup \{ |P(A) - Q(A)|�: A\text{ is an event to which probabilities are assigned.} \}.$

where

$D_{KL}^{(e)}(P||Q)$

is the Kullback–Leibler divergence in nats and

$\sup_A |P(A) - Q(A)| \,$

is the total variation distance.

Other inequalities

Hirschman uncertainty

Main article: Hirschman uncertainty

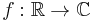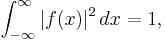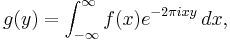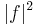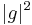In 1957,^[6] Hirschman showed that for a (reasonably well-behaved) function $f:\mathbb R \rightarrow \mathbb C$ such that $\int_{-\infty}^\infty |f(x)|^2\,dx = 1,$ and its Fourier transform $g(y)=\int_{-\infty}^\infty f(x) e^{-2 \pi i x y}\,dx,$ the sum of the differential entropies of $|f|^2$ and $|g|^2$ is non-negative, i.e.

$-\int_{-\infty}^\infty |f(x)|^2 \log |f(x)|^2 \,dx -\int_{-\infty}^\infty |g(y)|^2 \log |g(y)|^2 \,dy \ge 0.$

Hirschman conjectured, and it was later proved,^[7] that a sharper bound of 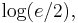$\log(e/2),$ which is attained in the case of a Gaussian distribution, could replace the right-hand side of this inequality. This is especially significant since it implies, and is stronger than, Weyl's formulation of Heisenberg's uncertainty principle.

Tao's inequality

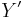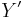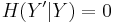Given discrete random variables $X$ , $Y$ , and $Y'$ , such that $X$ takes values only in the interval [−1, 1] and $Y'$ is determined by $Y$ (so that $H(Y'|Y)=0$ ), we have^[8]^[9]

$\mathbb E \big( \big| \mathbb E(X|Y') - \mathbb E(X|Y) \big| \big) \le \sqrt { 2 \log 2 \, I(X;Y|Y') },$

relating the conditional expectation to the conditional mutual information. This is a simple consequence of Pinsker's inequality. (Note: the correction factor log 2 inside the radical arises because we are measuring the conditional mutual information in bits rather than nats.)

References

^ R.Yeung,Y.Yan,ITIP – Information Theoretic Inequality Prover
^ R.Pulikkoonattu,E.Perron,S.Diggavi, Xitip – Information Theoretic Inequalities Prover
^ Zhang, Z.; Yeung, R. W. (1997). "A non-Shannon-type conditional inequality of information quantities". IEEE Transactions on Information Theory (New York) 43 (6): 1982. doi:10.1109/18.641561.
^ Makarychev, K.; et al. (2002). "A new class of non-Shannon-type inequalities for entropies". Communications in Information and Systems 2 (2): 147–166. http://www.cs.princeton.edu/~ymakaryc/papers/nonshann.pdf.
^ Fuchs, Aimé; Letta, Giorgio (1970). "L'inégalité de Kullback. Application à la théorie de l'estimation". Séminaire de probabilités (Strasbourg) 4: 108–131. MR 267669.
^ Hirschman, I. I. (1957). "A Note on Entropy". American Journal of Mathematics 79 (1): 152–156. doi:10.2307/2372390. JSTOR 2372390.
^ Beckner, W. (1975). "Inequalities in Fourier Analysis". Annals of Mathematics 102 (6): 159–182. doi:10.2307/1970980. JSTOR 1970980.
^ Tao, T. (2006). "Szemeredi's regularity lemma revisited". Contrib. Discrete Math. 1: 8–28. arXiv:math/0504472.
^ Ahlswede, Rudolf (2007). "The final form of Tao's inequality relating conditional expectation and conditional mutual information". Advances in Mathematics of Communications 1 (2): 239–242. doi:10.3934/amc.2007.1.239.

External links

Thomas M. Cover, Joy A. Thomas. Elements of Information Theory, Chapter 16, "Inequalities in Information Theory" John Wiley & Sons, Inc. 1991 Print ISBN 0471062596 Online ISBN 0471200611 pdf
Amir Dembo, Thomas M. Cover, Joy A. Thomas. Information Theoretic Inequalities. IEEE Transactions on Information Theory, Vol. 37, No. 6, November 1991. pdf