Indeterminate (variable)

In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a function argument, or being summed or integrated over, or any other type of bound variable. Indeterminates are used to build formal objects such as polynomials, formal power series, or elements of a free group.

Example

The distinction between an unknown and an indeterminate can be illustrated as follows.

1. Let $x$ be an unknown satisfying

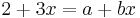$2%2B3x=a%2Bbx \,$ ,

where a and b are given numbers (or parameters). Then, provided b is not 3, we can solve for x, to find

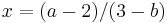$x=(a-2)/(3-b) \,$ ,

while for b = 3 the problem either has no solution at all, or, if also a = 2, it admits any value for x as solution.

2. Let $X$ be an indeterminate, and a, b as above. Then

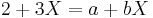$2%2B3X=a%2BbX \,$ ,

does not hold unless a = 2 and b = 3. This is because X is not, and does not designate, a number; the only way 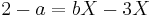$2-a=bX-3X$ can hold is when both sides of the equation are 0.

References

This article incorporates material from indeterminate on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Indeterminate (variable)

Example

See also

References