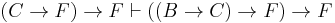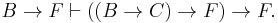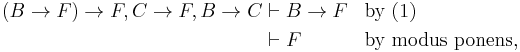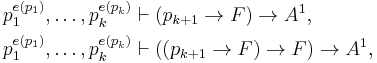Implicational propositional calculus

In mathematical logic, the implicational propositional calculus is a version of classical propositional calculus which uses only one connective, called implication or conditional. In formulas, this binary operation is indicated by "implies", "if ..., then ...", "→", "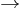 $\rightarrow \!$ ", etc..

1 Virtual completeness as an operator
2 Axiom system
3 Basis properties
4 Completeness
- 4.1 Proof
5 See also
6 References

Virtual completeness as an operator

Implication alone is not functionally complete as a logical operator because one cannot form all other two-valued truth functions from it. However, if one has a propositional formula which is known to be false and uses that as if it were a nullary connective for falsity, then one can define all other truth functions. So implication is virtually complete as an operator. If P,Q, and F are propositions and F is known to be false, then:

¬P is equivalent to P → F
P ∧ Q is equivalent to (P → (Q → F)) → F
P ∨ Q is equivalent to (P → Q) → Q
P ↔ Q is equivalent to ((P → Q) → ((Q → P) → F)) → F

More generally, since the above operators are known to be functionally complete, it follows that any truth function can be expressed in terms of "→" and "F", if we have a proposition F which is known to be false.

It is worth noting that F is not definable from → and arbitrary sentence variables: any formula constructed from → and propositional variables must receive the value true when all of its variables are evaluated to true. It follows as a corollary that {→} is not functionally complete. It cannot, for example, be used to define the two-place truth function that always returns false.

Axiom system

Axiom schema 1 is P → (Q → P).
Axiom schema 2 is (P → (Q → R)) → ((P → Q) → (P → R)).
Axiom schema 3 (Peirce's law) is ((P → Q) → P) → P.
The one non-nullary rule of inference (modus ponens) is: from P and P → Q infer Q.

Where in each case, P, Q, and R may be replaced by any formulas which contain only "→" as a connective. If Γ is a set of formulas and A a formula, then 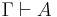$\Gamma\vdash A$ means that A is derivable using the axioms and rules above and formulas from Γ as additional hypotheses.

Basis properties

Since all axioms and rules of the calculus are schemata, derivation is closed under substitution:

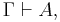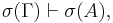
If $\Gamma\vdash A,$ then $\sigma(\Gamma)\vdash\sigma(A),$

where σ is any substitution (of formulas using only implication).

The implicational propositional calculus also satisfies the deduction theorem:

If 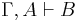$\Gamma,A\vdash B$ , then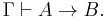 $\Gamma\vdash A\to B.$

As explained in the deduction theorem article, this holds for any axiomatic extension of the system consisting of axioms 1 and 2 above and modus ponens.

Completeness

The implicational propositional calculus is semantically complete with respect to the usual two-valued semantics of classical propositional logic. That is, if Γ is a set of implicational formulas, and A is an implicational formula entailed by Γ, then 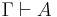$\Gamma\vdash A$ .

Proof

A proof of the completeness theorem is outlined below. First, using the compactness theorem and the deduction theorem, we may reduce the completeness theorem to its special case with empty Γ, i.e., we only need to show that every tautology is derivable in the system.

The proof is similar to completeness of full propositional logic, but it also uses the following idea to overcome the functional incompleteness of implication. If A and F are formulas, then A → F is equivalent to (¬A*) ∨ F, where A* is the result of replacing in A all, some, or none of the occurrences of F by falsity. Similarly, (A → F) → F is equivalent to A* ∨ F. So under some conditions, one can use them as substitutes for saying A* is false or A* is true respectively.

We first observe some basic facts about derivability:

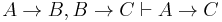
$A\to B,B\to C\vdash A\to C$

(1)

Indeed, we can derive A → (B → C) using Axiom 1, and then derive A → C by modus ponens (twice) from Ax. 2.

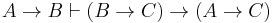
$A\to B\vdash(B\to C)\to(A\to C)$

(2)

This follows from (1) by the deduction theorem.

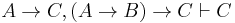
$A\to C,(A\to B)\to C\vdash C$

(3)

If we further assume C → B, we can derive A → B using (1), then we derive C by modus ponens. This shows 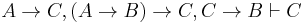$A\to C,(A\to B)\to C,C\to B\vdash C$ , and the deduction theorem gives 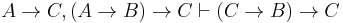$A\to C,(A\to B)\to C\vdash(C\to B)\to C$ . We apply Ax. 3 to obtain (3).

Let F be an arbitrary fixed formula. For any formula A, we define A⁰ = (A → F) and A¹ = ((A → F) → F). Let us consider only formulas in propositional variables p₁, ..., p_n. We claim that for every formula A in these variables and every truth assignment e,

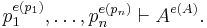
$p_1^{e(p_1)},\dots,p_n^{e(p_n)}\vdash A^{e(A)}.$

(4)

We prove (4) by induction on A. The base case A = p_i is trivial. Let A = (B → C). We distinguish three cases:

e(C) = 1. Then also e(A) = 1. We have

$(C\to F)\to F\vdash((B\to C)\to F)\to F$

by applying (2) twice to the axiom C → (B → C). Since we have derived (C → F) → F by the induction hypothesis, we can infer ((B → C) → F) → F.
e(B) = 0. Then again e(A) = 1. The deduction theorem applied to (3) gives

$B\to F\vdash((B\to C)\to F)\to F.$

Since we have derived B → F by the induction hypothesis, we can infer ((B → C) → F) → F.
e(B) = 1 and e(C) = 0. Then e(A) = 0. We have

$\begin{align}(B\to F)\to F,C\to F,B\to C&\vdash B\to F&&\text{by (1)}\\&\vdash F&&\text{by modus ponens,}\end{align}$

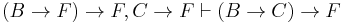thus $(B\to F)\to F,C\to F\vdash(B\to C)\to F$ by the deduction theorem. We have derived (B → F) → F and C → F by the induction hypothesis, hence we can infer (B → C) → F. This completes the proof of (4).

Now let A be a tautology in variables p₁, ..., p_n. We will prove by reverse induction on k = n,...,0 that for every assignment e,

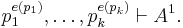
$p_1^{e(p_1)},\dots,p_k^{e(p_k)}\vdash A^1.$

(5)

The base case k = n is a special case of (4). Assume that (5) holds for k + 1, we will show it for k. By applying deduction theorem to the induction hypothesis, we obtain

$\begin{align}p_1^{e(p_1)},\dots,p_k^{e(p_k)}&\vdash(p_{k%2B1}\to F)\to A^1,\\ p_1^{e(p_1)},\dots,p_k^{e(p_k)}&\vdash((p_{k%2B1}\to F)\to F)\to A^1,\end{align}$

by first setting e(p_k+1) = 0 and second setting e(p_k+1) = 1. From this we derive (5) using (3).

For k = 0 we obtain that the formula A¹, i.e., (A → F) → F, is provable without assumptions. Recall that F was an arbitrary formula, thus we can choose F = A, which gives us provability of the formula (A → A) → A. Since A → A is provable by the deduction theorem, we can infer A.

This proof is constructive. That is, given a tautology, one could actually follow the instructions and create a proof of it from the axioms. However, the length of such a proof increases exponentially with the number of propositional variables in the tautology, hence it is not a practical method for any but the very shortest tautologies.

References

Mendelson, Elliot (1997) Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall.