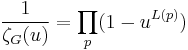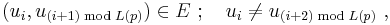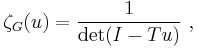Ihara zeta function

In mathematics, the Ihara zeta-function is a zeta function associated with a finite graph. It closely resembles the Selberg zeta-function, and is used to relate closed paths to the spectrum of the adjacency matrix. The Ihara zeta-function was first defined by Yasutaka Ihara in the 1960s in the context of discrete subgroups of the two-by-two p-adic special linear group. Jean-Pierre Serre suggested in his book Trees that Ihara's original definition can be reinterpreted graph-theoretically. It was Toshikazu Sunada who put this suggestion into practice (1985). A regular graph is a Ramanujan graph if and only if its Ihara zeta function satisfies an analogue of the Riemann hypothesis.

Contents

1 Definition
2 Ihara's formula
3 Applications
4 References

Definition

The Ihara zeta-function can be defined by a formula analogous to the Euler product for the Riemann zeta function:

$\frac{1}{\zeta_G(u)} = \prod_{p} ({1 - u^{L(p)}})$

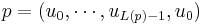This product is taken over all prime walks p of the graph $G = (V, E)$ - that is, closed cycles $p = (u_0, \cdots, u_{L(p)-1}, u_0)$ such that

$(u_i, u_{(i%2B1)\bmod L(p)}) \in E~; \quad u_i \neq u_{(i%2B2) \bmod L(p)~},$

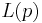and $L(p)$ is the length of cycle p, as used in the formulae above.

Ihara's formula

The Ihara zeta-function is in fact always the reciprocal of a polynomial:

$\zeta_G(u) = \frac{1}{\det (I-Tu)}~,$

where T is Hashimoto's edge adjacency operator. Hyman Bass gave a determinant formula involving the adjacency operator.

Applications

The Ihara zeta-function plays an important role in the study of free groups, spectral graph theory, and dynamical systems, especially symbolic dynamics.

References

Y. Ihara (1966). "On discrete subgroups of the two by two projective linear group over 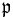${\mathfrak p}$ -adic fields". J. Math. Soc. Japan 18: 219–235.
T. Sunada (1985). L-functions in geometry and some applications. "Curvature and Topology of Riemannian Manifolds". Lecture Notes in Math.. Lecture Notes in Mathematics 1201: 266–284. doi:10.1007/BFb0075662. ISBN 978-3-540-16770-9.

H. Bass (1992). "The Ihara-Selberg zeta function of a tree lattice". International. J. Math. 3 (6): 717–797. doi:10.1142/S0129167X92000357.

Dennis A. Hejhal; Joel Friedman, Martin C. Gutzwiller, Andrew M. Odlyzko (1999). Emerging Applications of Number Theory. Springer. p. 677. ISBN 0387988246.