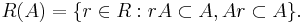Idealizer

In mathematics, the idealizer R(A) of an additive subgroup A of a ring R is the largest subring of R that contains A as a two-sided ideal. One has

$R(A) = \{r \in R�: rA\subset A, Ar\subset A\}. \,$

Example: The multiplier algebra M(A) of a C^*-algebra A is isomorphic to the idealizer of π(A) where π is any faithful nondegenerate representation of A on a Hilbert space H.