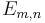Hypercube

Perspective projections
Cube (3-cube) Tesseract (4-cube)

In geometry, a hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.

An n-dimensional hypercube is also called an n-cube. The term "measure polytope" is also used, notably in the work of H.S.M. Coxeter (originally from Elte, 1912[1]), but it has now been superseded.

The hypercube is the special case of a hyperrectangle (also called an orthotope).

A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2n points in Rn with coordinates equal to 0 or 1 is called "the" unit hypercube.

Contents

Construction

0 – A point is a hypercube of dimension zero.
1 – If one moves this point one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one.
2 – If one moves this line segment its length in a perpendicular direction from itself; it sweeps out a 2-dimensional square.
3 – If one moves the square one unit length in the direction perpendicular to the plane it lies on, it will generate a 3-dimensional cube.
4 – If one moves the cube one unit length into the fourth dimension, it generates a 4-dimensional unit hypercube (a unit tesseract).

This can be generalized to any number of dimensions. This process of sweeping out volumes can be formalized mathematically as a Minkowski sum: the d-dimensional hypercube is the Minkowski sum of d mutually perpendicular unit-length line segments, and is therefore an example of a zonotope.

The 1-skeleton of a hypercube is a hypercube graph.

Coordinates

A unit hypercube of n dimensions is the convex hull of the points given by all sign permutations of the Cartesian coordinates 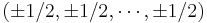(\pm 1/2, \pm 1/2, \cdots, \pm 1/2). It has an edge length of 1 and an n-dimensional volume of 1.

An n-dimensional hypercube is also often regarded as the convex hull of all sign permutations of the coordinates 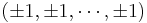(\pm 1, \pm 1, \cdots, \pm 1). This form is often chosen due to ease of writing out the coordinates. Its edge length is 2, and its n-dimensional volume is 2n.

Related families of polytopes

The hypercubes are one of the few families of regular polytopes that are represented in any number of dimensions.

The hypercube (offset) family is one of three regular polytope families, labeled by Coxeter as γn. The other two are the hypercube dual family, the cross-polytopes, labeled as βn, and the simplices, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.

Another related family of semiregular and uniform polytopes is the demihypercubes, which are constructed from hypercubes with alternate vertices deleted and simplex facets added in the gaps, labeled as hγn.

Elements

A hypercube of dimension n has 2n "sides" (a 1-dimensional line has 2 end points; a 2-dimensional square has 4 sides or edges; a 3-dimensional cube has 6 2-dimensional faces; a 4-dimensional tesseract has 8 cells). The number of vertices (points) of a hypercube is 2n (a cube has 23 vertices, for instance).

A simple formula to calculate the number of "n-2"-faces in an n-dimensional hypercube is: 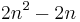2n^{2}-2n

The number of m-dimensional hypercubes (just referred to as m-cube from here on) on the boundary of an n-cube is

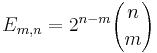E_{m,n} = 2^{n-m}{n \choose m} ,     where 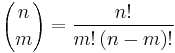{n \choose m}=\frac{n!}{m!\,(n-m)!} and n! denotes the factorial of n.

For example, the boundary of a 4-cube (n=4) contains 8 cubes (3-cubes), 24 squares (2-cubes), 32 lines (1-cubes) and 16 vertices (0-cubes).

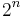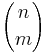This identity can be proved by combinatorial arguments; each of the 2^n vertices defines a vertex in a m-dimensional boundary. There are {n \choose m} ways of choosing which lines ("sides") that defines the subspace that the boundary is in. But, each side is counted 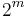2^m times since it has that many vertices, we need to divide with this number. Hence the identity above.

These numbers can also be generated by the linear recurrence relation

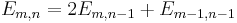E_{m,n} = 2E_{m,n-1} %2B E_{m-1,n-1} \!,     with 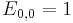E_{0,0} = 1 \!,     and undefined elements = 0.

For example, extending a square via its 4 vertices adds one extra line (edge) per vertex, and also adds the final second square, to form a cube, giving 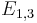E_{1,3} \! = 12 lines in total.

Hypercube elements E_{m,n} \!
m 0 1 2 3 4 5 6 7 8 9 10
n γn n-cube Names
Schläfli symbol
Coxeter-Dynkin		 Vertices Edges Faces Cells (3-faces) 4-faces (Hypercells) 5-faces 6-faces 7-faces 8-faces 9-faces 10-faces
0 γ0 0-cube Point
-		 1                    
1 γ1 1-cube Line segment
{}
 2 1                  
2 γ2 2-cube Square
Tetragon
{4}
 4 4 1                
3 γ3 3-cube Cube
Hexahedron
{4,3}
 8 12 6 1              
4 γ4 4-cube Tesseract
Octachoron
{4,3,3}
 16 32 24 8 1            
5 γ5 5-cube Penteract
Decateron
{4,3,3,3}
 32 80 80 40 10 1          
6 γ6 6-cube Hexeract
Dodecapeton
{4,3,3,3,3}
 64 192 240 160 60 12 1        
7 γ7 7-cube Hepteract
Tetradeca-7-tope
{4,3,3,3,3,3}
 128 448 672 560 280 84 14 1      
8 γ8 8-cube Octeract
Hexadeca-8-tope
{4,3,3,3,3,3,3}
 256 1024 1792 1792 1120 448 112 16 1    
9 γ9 9-cube Enneract
Octadeca-9-tope
{4,3,3,3,3,3,3,3}
 512 2304 4608 5376 4032 2016 672 144 18 1  
10 γ10 10-cube Dekeract
icosa-10-tope
{4,3,3,3,3,3,3,3,3}
 1024 5120 11520 15360 13440 8064 3360 960 180 20 1

Graphs

An n-cube can be projected inside a regular 2n-gonal polygon by a skew orthogonal projection, shown here from the line segment to the 12-cube.

Petrie polygon Orthographic projections

Line segment
Square
Cube
4-cube (tesseract)

5-cube (penteract)
6-cube (hexeract)
7-cube (hepteract)
8-cube (octeract)

9-cube (enneract)
10-cube (dekeract)
11-cube (hendekeract)
12-cube (dodekeract)

Relation to n-simplices

The graph of the n-hypercube's edges is isomorphic to the Hasse diagram of the (n-1)-simplex's face lattice. This can be seen by orienting the n-hypercube so that two opposite vertices lie vertically, corresponding to the (n-1)-simplex itself and the null polytope, respectively. Each vertex connected to the top vertex then uniquely maps to one of the (n-1)-simplex's facets (n-2 faces), and each vertex connected to those vertices maps to one of the simplex's n-3 faces, and so forth, and the vertices connected to the bottom vertex map to the simplex's vertices.

This relation may be used to generate the face lattice of an (n-1)-simplex efficiently, since face lattice enumeration algorithms applicable to general polytopes are more computationally expensive.

See also

Notes

  1. ^ Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen  Chapter IV, five dimensional semiregular polytope [1]

References

External links