Hypercomputation
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms (see also supertask). The term "super-Turing computation" appeared in a 1995 Science paper by Hava Siegelmann. The term "hypercomputation" was introduced in 1999 by Jack Copeland and Diane Proudfoot.[1]
The terms are not quite synonymous: "super-Turing computation" usually implies that the proposed model is supposed to be physically realizable, while "hypercomputation" does not.
Contents |
History
A model more powerful than Turing machines was introduced by Alan Turing in his 1939 paper Systems of logic based on ordinals. This paper investigated mathematical systems in which an oracle was available, which could compute a single arbitrary (non-recursive) function from naturals to naturals. He used this device to prove that even in those more powerful systems, undecidability is still present. Turing's oracle machines are strictly mathematical abstractions, and are not physically realizable.[2]
Hypercomputation and the Church–Turing thesis
The Church–Turing thesis states that any function that is algorithmically computable can be computed by a Turing machine. Hypercomputers compute functions that a Turing machine cannot, hence, not computable in the Church-Turing sense.
An example of a problem a Turing machine cannot solve is the halting problem. A Turing machine cannot decide if an arbitrary program halts or runs forever. Some proposed hypercomputers can simulate the program for an infinite number of steps and tell the user whether or not the program halted.
Hypercomputer proposals
- A Turing machine that can complete infinitely many steps. Simply being able to run for an unbounded number of steps does not suffice. One mathematical model is the Zeno machine (inspired by Zeno's paradox). The Zeno machine performs its first computation step in (say) 1 minute, the second step in ½ minute, the third step in ¼ minute, etc. By summing 1+½+¼+... (a geometric series) we see that the machine performs infinitely many steps in a total of 2 minutes. However, some people claim that, following the reasoning from Zeno's paradox, Zeno machines are not just physically impossible, but logically impossible.[3] Another example uses time dilation to allow a computer to spend an infinite amount of time performing a computation while a finite amount of time passes for an observer (it would require an infinite amount of energy to perform this calculation—see Malament-Hogarth spacetime).
- Turing's original oracle machines, defined in Turing 1939.
- In mid 1960s, E Mark Gold and Hilary Putnam independently proposed models of inductive inference (the "limiting recursive functionals"[4] and "trial-and-error predicates",[5] respectively). These models enable some nonrecursive sets of numbers or languages (including all recursively enumerable sets of languages) to be "learned in the limit"; whereas, by definition, only recursive sets of numbers or languages could be identified by a Turing machine. While the machine will stabilize to the correct answer on any learnable set in some finite time, it can only identify it as correct if it is recursive; otherwise, the correctness is established only by running the machine forever and noting that it never revises its answer. Putnam identified this new interpretation as the class of "empirical" predicates, stating: "if we always 'posit' that the most recently generated answer is correct, we will make a finite number of mistakes, but we will eventually get the correct answer. (Note, however, that even if we have gotten to the correct answer (the end of the finite sequence) we are never sure that we have the correct answer.)"[5] L. K. Schubert's 1974 paper "Iterated Limiting Recursion and the Program Minimization Problem" [6] studied the effects of iterating the limiting procedure; this allows any arithmetic predicate to be computed. Schubert wrote, "Intuitively, iterated limiting identification might be regarded as higher-order inductive inference performed collectively by an ever-growing community of lower order inductive inference machines."
- A real computer (a sort of idealized analog computer) can perform hypercomputation[7] if physics admits general real variables (not just computable reals), and these are in some way "harnessable" for computation. This might require quite bizarre laws of physics (for example, a measurable physical constant with an oracular value, such as Chaitin's constant), and would at minimum require the ability to measure a real-valued physical value to arbitrary precision despite thermal noise and quantum effects.
- A proposed technique known as fair nondeterminism or unbounded nondeterminism may allow the computation of noncomputable functions.[8] There is dispute in the literature over whether this technique is coherent, and whether it actually allows noncomputable functions to be "computed".
- It seems natural that the possibility of time travel (existence of closed timelike curves (CTCs)) makes hypercomputation possible by itself. However, this is not so since a CTC does not provide (by itself) the unbounded amount of storage that an infinite computation would require. Nevertheless, there are spacetimes in which the CTC region can be used for relativistic hypercomputation.[9] Access to a CTC may allow the rapid solution to PSPACE-complete problems, a complexity class which while Turing-decidable is generally considered computationally intractable.[10][11]
- According to a 1992 paper,[12] a computer operating in a Malament-Hogarth spacetime or in orbit around a rotating black hole[13] could theoretically perform non-Turing computations.[14][15]
- In 1994, Hava Siegelmann proved that her new (1991) computational model, the Artificial Recurrent Neural Network (ARNN), could perform hypercomputation (using infinite precision real weights for the synapses). It is based on evolving an artificial neural network through a discrete, infinite succession of states.[16]
- The infinite time Turing machine is a generalization of the Zeno machine, that can perform infinitely long computations whose steps are enumerated by potentially transfinite ordinal numbers. It models an otherwise-ordinary Turing machine for which non-halting computations are completed by entering a special state reserved for reaching a limit ordinal and to which the results of the preceding infinite computation are available.[17]
- Jan van Leeuwen and Jiří Wiedermann wrote a 2000 paper[18] suggesting that the Internet should be modeled as a nonuniform computing system equipped with an advice function representing the ability of computers to be upgraded.
- A symbol sequence is computable in the limit if there is a finite, possibly non-halting program on a universal Turing machine that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π and of every other computable real, but still excludes all noncomputable reals. Traditional Turing machines cannot edit their previous outputs; generalized Turing machines, as defined by Jürgen Schmidhuber, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges, that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt Gödel (1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problem could be solved. Schmidhuber ([19][20]) uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everything. Generalized Turing machines can solve the halting problem by evaluating a Specker sequence.
- A quantum mechanical system which somehow uses an infinite superposition of states to compute a non-computable function.[21] This is not possible using the standard qubit-model quantum computer, because it is proven that a regular quantum computer is PSPACE-reducible (a quantum computer running in polynomial time can be simulated by a classical computer running in polynomial space).[22]
- In 1970, E.S. Santos defined a class of fuzzy logic-based "fuzzy algorithms" and "fuzzy Turing machines".[23] Subsequently, L. Biacino and G. Gerla showed that such a definition would allow the computation of nonrecursive languages; they suggested an alternative set of definitions without this difficulty.[24] Jiří Wiedermann analyzed the capabilities of Santos' original proposal in 2004.[25]
- Dmytro Taranovsky has proposed a finitistic model of traditionally non-finitistic branches of analysis, built around a Turing machine equipped with a rapidly increasing function as its oracle. By this and more complicated models he was able to give an interpretation of second-order arithmetic.[26]
Analysis of capabilities
Many hypercomputation proposals amount to alternative ways to read an oracle or advice function embedded into an otherwise classical machine. Others allow access to some higher level of the arithmetic hierarchy. For example, supertasking Turing machines, under the usual assumptions, would be able to compute any predicate in the truth-table degree containing 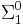 or
or 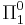 . Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree, which is known to be
. Limiting-recursion, by contrast, can compute any predicate or function in the corresponding Turing degree, which is known to be 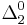 . Gold further showed that limiting partial recursion would allow the computation of precisely the
. Gold further showed that limiting partial recursion would allow the computation of precisely the 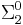 predicates.
predicates.
| Model | Computable predicates | Notes | Refs |
|---|---|---|---|
| supertasking | tt(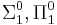 ) ) |
dependent on outside observer | [27] |
| limiting/trial-and-error | 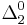 |
[4] | |
| iterated limiting (k times) | 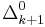 |
[6] | |
| Blum-Shub-Smale machine | incomparable with traditional computable real functions. | [28] | |
| Malament-Hogarth spacetime | HYP | Dependent on spacetime structure | [29] |
| Analog recurrent neural network | ![\Delta^0_1[f]](/2012-wikipedia_en_all_nopic_01_2012/I/dd9474960ab9e8e906912bdf3e92b108.png) |
f is an advice function giving connection weights; size is bounded by runtime | [30][31] |
| Infinite time Turing machine | 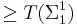 |
[32] | |
| Classical fuzzy Turing machine |  |
For any computable t-norm | [33] |
| Increasing function oracle | 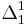 |
For the one-sequence model; 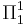 are r.e. are r.e. |
[26] |
Taxonomy of "super-recursive" computation methodologies
Burgin has collected a list of what he calls "super-recursive algorithms" (from Burgin 2005: 132):
- limiting recursive functions and limiting partial recursive functions (E. M. Gold[4])
- trial and error predicates (Hilary Putnam[5])
- inductive inference machines (Carl Herbert Smith)
- inductive Turing machines (one of Burgin's own models)
- limit Turing machines (another of Burgin's models)
- trial-and-error machines (Ja. Hintikka and A. Mutanen [34])
- general Turing machines (J. Schmidhuber[20])
- Internet machines (van Leeuwen, J. and Wiedermann, J.[18])
- evolutionary computers, which use DNA to produce the value of a function (Darko Roglic[35])
- fuzzy computation (Jiří Wiedermann[25])
- evolutionary Turing machines (Eugene Eberbach[36])
In the same book, he presents also a list of "algorithmic schemes":
- Turing machines with arbitrary oracles (Alan Turing)
- Transrecursive operators (Borodyanskii and Burgin[37])
- machines that compute with real numbers (L. Blum, F. Cucker, M. Shub, and S. Smale)
- neural networks based on real numbers (Hava Siegelmann)
Criticism
Martin Davis, in his writings on hypercomputation [38] [39] refers to this subject as "a myth" and offers counter-arguments to the physical realizability of hypercomputation. As for its theory, he argues against the claims that this is a new field founded in 1990s. This point of view relies on the history of computability theory (degrees of unsolvability, computability over functions, real numbers and ordinals), as also mentioned above.
Andrew Hodges wrote a critical commentary[40] on Copeland and Proudfoot's article[1].
See also
References
- ^ a b Copeland and Proudfoot, Alan Turing's forgotten ideas in computer science. Scientific American, April 1999
- ^ "Let us suppose that we are supplied with some unspecified means of solving number-theoretic problems; a kind of oracle as it were. We shall not go any further into the nature of this oracle apart from saying that it cannot be a machine" (Undecidable p. 167, a reprint of Turing's paper Systems of Logic Based On Ordinals)
- ^ These models have been independently developed by many different authors, including Hermann Weyl (1927). Philosophie der Mathematik und Naturwissenschaft.; the model is discussed in Shagrir, O. (June 2004). "Super-tasks, accelerating Turing machines and uncomputability". Theor. Comput. Sci. 317, 1-3 317: 105–114. doi:10.1016/j.tcs.2003.12.007. http://edelstein.huji.ac.il/staff/shagrir/papers/Supertasks_Accelerating_Turing_Machines_and_Uncomputability.pdf. and in Petrus H. Potgieter (July 2006). "Zeno machines and hypercomputation". Theoretical Computer Science 358 (1): 23–33. doi:10.1016/j.tcs.2005.11.040.
- ^ a b c E. M. Gold (1965). "Limiting Recursion". Journal of Symbolic Logic 30 (1): 28–48. doi:10.2307/2270580. JSTOR 2270580., E. Mark Gold (1967). "Language identification in the limit". Information and Control 10 (5): 447–474. doi:10.1016/S0019-9958(67)91165-5.
- ^ a b c Hilary Putnam (1965). "Trial and Error Predicates and the Solution to a Problem of Mostowksi". Journal of Symbolic Logic 30 (1): 49–57. doi:10.2307/2270581. JSTOR 2270581.
- ^ a b L. K. Schubert (July 1974). "Iterated Limiting Recursion and the Program Minimization Problem". Journal of the ACM 21 (3): 436–445. doi:10.1145/321832.321841. http://portal.acm.org/citation.cfm?id=321832.321841.
- ^ Arnold Schönhage, "On the power of random access machines", in Proc. Intl. Colloquium on Automata, Languages, and Programming (ICALP), pages 520-529, 1979. Source of citation: Scott Aaronson, "NP-complete Problems and Physical Reality"[1] p. 12
- ^ Edith Spaan, Leen Torenvliet and Peter van Emde Boas (1989). "Nondeterminism, Fairness and a Fundamental Analogy". EATCS bulletin 37: 186–193.
- ^ Hajnal Andréka, István Németi and Gergely Székely, Closed Timelike Curves in Relativistic Computation, 2011.[2]
- ^ Todd A. Brun, Computers with closed timelike curves can solve hard problems, Found.Phys.Lett. 16 (2003) 245-253.[3]
- ^ S. Aaronson and J. Watrous. Closed Timelike Curves Make Quantum and Classical Computing Equivalent [4]
- ^ Hogarth, M., 1992, ‘Does General Relativity Allow an Observer to View an Eternity in a Finite Time?’, Foundations of Physics Letters, 5, 173–181.
- ^ István Neméti; Hajnal Andréka (2006). "Can General Relativistic Computers Break the Turing Barrier?". Logical Approaches to Computational Barriers, Second Conference on Computability in Europe, CiE 2006, Swansea, UK, June 30-July 5, 2006. Proceedings. Lecture Notes in Computer Science. 3988. Springer. doi:10.1007/11780342.
- ^ Etesi, G., and Nemeti, I., 2002 'Non-Turing computations via Malament-Hogarth space-times', Int.J.Theor.Phys. 41 (2002) 341–370, Non-Turing Computations via Malament-Hogarth Space-Times:.
- ^ Earman, J. and Norton, J., 1993, ‘Forever is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes’, Philosophy of Science, 5, 22–42.
- ^ Verifying Properties of Neural Networks p.6
- ^ Joel David Hamkins and Andy Lewis, Infinite time Turing machines, Journal of Symbolic Logic, 65(2):567-604, 2000.[5]
- ^ a b Jan van Leeuwen; Jiří Wiedermann (September 2000). "On Algorithms and Interaction". MFCS '00: Proceedings of the 25th International Symposium on Mathematical Foundations of Computer Science. Springer-Verlag.
- ^ Jürgen Schmidhuber (2000). "Algorithmic Theories of Everything". Sections in: Hierarchies of generalized Kolmogorov complexities and nonenumerable universal measures computable in the limit. International Journal of Foundations of Computer Science ():587-612 (). Section 6 in: the Speed Prior: A New Simplicity Measure Yielding Near-Optimal Computable Predictions. in J. Kivinen and R. H. Sloan, editors, Proceedings of the 15th Annual Conference on Computational Learning Theory (COLT ), Sydney, Australia, Lecture Notes in Artificial Intelligence, pages 216--228. Springer, . 13 (4): 1–5. arXiv:quant-ph/0011122.
- ^ a b J. Schmidhuber (2002). "Hierarchies of generalized Kolmogorov complexities and nonenumerable universal measures computable in the limit". International Journal of Foundations of Computer Science 13 (4): 587–612. doi:10.1142/S0129054102001291. http://www.idsia.ch/~juergen/kolmogorov.html.
- ^ There have been some claims to this effect; see Tien Kieu (2003). "Quantum Algorithm for the Hilbert's Tenth Problem". Int. J. Theor. Phys. 42 (7): 1461–1478. arXiv:quant-ph/0110136. doi:10.1023/A:1025780028846.. & the ensuing literature. Errors have been pointed out in Kieu's approach by Warren D. Smith in Three counterexamples refuting Kieu’s plan for “quantum adiabatic hypercomputation”; and some uncomputable quantum mechanical tasks
- ^ Bernstein and Vazirani, Quantum complexity theory, SIAM Journal on Computing, 26(5):1411-1473, 1997. [6]
- ^ Santos, Eugene S. (1970). "Fuzzy Algorithms". Information and Control 17 (4): 326–339. doi:10.1016/S0019-9958(70)80032-8.
- ^ Biacino, L.; Gerla, G. (2002). "Fuzzy logic, continuity and effectiveness". Archive for Mathematical Logic 41 (7): 643–667. doi:10.1007/s001530100128. ISSN 0933-5846.
- ^ a b Wiedermann, Jiří (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theor. Comput. Sci. 317 (1–3): 61–69. doi:10.1016/j.tcs.2003.12.004. http://portal.acm.org/citation.cfm?id=1011188.
- ^ a b Dmytro Taranovsky (July 17, 2005). "Finitism and Hypercomputation". http://web.mit.edu/dmytro/www/FinitismPaper.htm. Retrieved Apr 26, 2011.
- ^ Petrus H. Potgieter (July 2006). "Zeno machines and hypercomputation". Theoretical Computer Science 358 (1): 23–33. doi:10.1016/j.tcs.2005.11.040.
- ^ Lenore Blum, Felipe Cucker, Michael Shub, and Stephen Smale. Complexity and Real Computation. ISBN 0387982817.
- ^ P. D. Welch (10-Sept-2006). The extent of computation in Malament-Hogarth spacetimes. arXiv:gr-qc/0609035.
- ^ Hava Siegelmann (April 1995). "Computation Beyond the Turing Limit". Science 268 (5210): 545–548. doi:10.1126/science.268.5210.545. PMID 17756722.
- ^ Hava Siegelmann; Eduardo Sontag (1994). "Analog Computation via Neural Networks". Theoretical Computer Science 131 (2): 331–360. doi:10.1016/0304-3975(94)90178-3.
- ^ Joel David Hamkins; Andy Lewis (2000). "Infinite Time Turing machines". Journal of Symbolic Logic 65 (2): 567=604. http://jdh.hamkins.org/Publications/2000e.
- ^ Jiří Wiedermann (June 4, 2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theoretical Computer Science (Elsevier Science Publishers Ltd. Essex, UK) 317 (1–3).
- ^ Hintikka, Ja; Mutanen, A. (1998). "An Alternative Concept of Computability". Language, Truth, and Logic in Mathematics. Dordrecht. pp. 174–188.
- ^ Darko Roglic (24–Jul–2007). "The universal evolutionary computer based on super-recursive algorithms of evolvability". arXiv:0708.2686 [cs.NE].
- ^ Eugene Eberbach (2002). "On expressiveness of evolutionary computation: is EC algorithmic?". Computational Intelligence, WCCI 1: 564–569. doi:10.1109/CEC.2002.1006988. http://www.computer.org/portal/web/csdl/doi/10.1109/CEC.2002.1006988.
- ^ Borodyanskii, Yu M; Burgin, M. S. (1994). "Operations and compositions in transrecursive operators". Cybernetics and Systems Analysis 30 (4): 473–478. doi:10.1007/BF02366556. http://www.springerlink.com/content/a70r23722wqu43t7/.
- ^ Davis, Martin, Why there is no such discipline as hypercomputation, Applied Mathematics and Computation, Volume 178, Issue 1, 1 July 2006, Pages 4–7, Special Issue on Hypercomputation
- ^ Davis, Martin (2004). "The Myth of Hypercomputation". Alan Turing: Life and Legacy of a Great Thinker. Springer.
- ^ Andrew Hodges (retrieved 23 September 2011). "The Professors and the Brainstorms". The Alan Turing Home Page. http://www.turing.org.uk/philosophy/sciam.html.
Further reading
- Hava Siegelmann (April 1995). "Computation Beyond the Turing Limit". Science 268 (5210): 545–548. doi:10.1126/science.268.5210.545. PMID 17756722.
- Turing, Alan (1939). "Systems of logic based on ordinals". Proc. London math. Soc. 45.
- Hava Siegelmann and Eduardo Sontag, “Analog Computation via Neural Networks,” Theoretical Computer Science 131, 1994: 331-360.
- Hava Siegelmann. Neural Networks and Analog Computation: Beyond the Turing Limit 1998 Boston: Birkhäuser (Book).
- Mike Stannett, The case for hypercomputation, Applied Mathematics and Computation, Volume 178, Issue 1, 1 July 2006, Pages 8–24, Special Issue on Hypercomputation
- Keith Douglas. Super-Turing Computation: a Case Study Analysis (PDF), M.S. Thesis, Carnegie Mellon University, 2003.
- L. Blum, F. Cucker, M. Shub, S. Smale, Complexity and Real Computation, Springer-Verlag 1997. General development of complexity theory for abstract machines that compute on real numbers instead of bits.
- On the computational power of neural nets
- Toby Ord. Hypercomputation: Computing more than the Turing machine can compute: A survey article on various forms of hypercomputation.
- Apostolos Syropoulos (2008), Hypercomputation: Computing Beyond the Church-Turing Barrier (preview), Springer. ISBN 9780387308869
- Burgin, M. S. (1983) Inductive Turing Machines, Notices of the Academy of Sciences of the USSR, v. 270, No. 6, pp. 1289–1293
- Mark Burgin (2005), Super-recursive algorithms, Monographs in computer science, Springer. ISBN 0387955690
- Cockshott, P. and Michaelson, G. Are there new Models of Computation? Reply to Wegner and Eberbach, The computer Journal, 2007
- Cooper, S. B. (2006). "Definability as hypercomputational effect". Applied Mathematics and Computation 178: 72–82. doi:10.1016/j.amc.2005.09.072. http://www.amsta.leeds.ac.uk/~pmt6sbc/preprints/hyp.comp.eff.pdf.
- Cooper, S. B.; Odifreddi, P. (2003). "Incomputability in Nature". In S. B. Cooper and S. S. Goncharov. Computability and Models: Perspectives East and West. Plenum Publishers, New York, Boston, Dordrecht, London, Moscow. pp. 137–160. http://www.amsta.leeds.ac.uk/~pmt6sbc/preprints/co.pdf.
- Copeland, J. (2002) Hypercomputation, Minds and machines, v. 12, pp. 461–502
- Martin Davis (2006), "The Church–Turing Thesis: Consensus and opposition". Proceedings, Computability in Europe 2006. Lecture notes in computer science, 3988 pp. 125–132
- Hagar, A. and Korolev, A., Quantum Hypercomputation—Hype or Computation?, (2007)
- Rogers, H. (1987) Theory of Recursive Functions and Effective Computability, MIT Press, Cambridge Massachusetts
- Volkmar Putz and Karl Svozil, Can a computer be "pushed" to perform faster-than-light?, (2010)