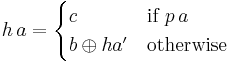Hylomorphism (computer science)
In computer science, and in particular functional programming, a hylomorphism is a recursive function, corresponding to the composition of an anamorphism (which first builds a set of results; also known as 'unfolding') and a catamorphism (which then folds these results into a final return value). Fusion of these two recursive computations into a single recursive pattern then avoids building the intermediate data structure. This is a particular form of the optimizing program transformation techniques collectively known as deforestation. The categorical dual of a hylomorphism is called a metamorphism, and is a catamorphism followed by an anamorphism.
Contents |
Formal definition
A hylomorphism 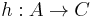 can be defined in terms of its separate anamorphic and catamorphic parts.
can be defined in terms of its separate anamorphic and catamorphic parts.
The anamorphic part can be defined in terms of a unary function 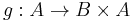 defining the list of elements in
defining the list of elements in  by repeated application ("unfolding"), and a predicate
by repeated application ("unfolding"), and a predicate 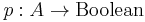 providing the terminating condition.
providing the terminating condition.
The catamorphic part can be defined as a combination of an initial value 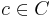 for the fold and a binary operator
for the fold and a binary operator 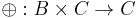 used to perform the fold.
used to perform the fold.
Thus a hylomorphism
(where 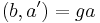 ) may be defined (assuming appropriate definitions of
) may be defined (assuming appropriate definitions of  ,
,  ,
,  ).
).
Notation
An abbreviated notation for the above hylomorphism is ![h = [\![(c, \oplus),(g, p)]\!]](/2012-wikipedia_en_all_nopic_01_2012/I/78bb0df139cf159d31584f873e712c4b.png) .
.
Hylomorphisms in practice
Lists
Lists are common data structures, as they naturally reflect linear computational processes arising in repeated (iterative) chain of applications of a function. As such, it is sometimes necessary (or, at least, preferable) to generate a temporary list of intermediate results before performing an operation to reduce this list to a single final results.
One example of a commonly encountered hylomorphism is the canonical factorial function.
factorial :: Integer -> Integer factorial n | n == 0 = 1 | n > 0 = n * factorial (n - 1)
In the previous example (written in Haskell, a purely functional programming language) it can be seen that this function, applied to any given valid input, will generate a linear call tree isomorphic to a list. For example, given n = 5 it will produce the following:
factorial 5 = 5 * (factorial 4) = 120 factorial 4 = 4 * (factorial 3) = 24 factorial 3 = 3 * (factorial 2) = 6 factorial 2 = 2 * (factorial 1) = 2 factorial 1 = 1 * (factorial 0) = 1 factorial 0 = 1
In this example, the anamorphic part of the process is the generation of the call tree which is isomorphic to the list [1, 1, 2, 3, 4, 5]. The catamorphism, then, is the calculation of the product of the elements of this list. Thus, in the notation given above, the factorial function may be written ![\text{factorial} = [\![(1,\times),(g, p)]\!]](/2012-wikipedia_en_all_nopic_01_2012/I/d0af47ab3f0b9db0edf4798ee12c3132.png) where
where 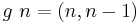 and
and 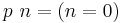 .
.
Trees
However, the term 'hylomorphism' does not apply solely to functions acting upon isomorphisms of lists. For example, a hylomorphism may also be defined by generating a non-linear call tree which is then collapsed. An example of such a function is the function to generate the nth term of the Fibonacci sequence.
fibonacci :: Integer -> Integer fibonacci n | n == 0 = 0 | n == 1 = 1 | n > 1 = fibonacci (n - 2) + fibonacci (n - 1)
This function, again applied to any valid input, will generate a call tree which is non-linear. In the example on the right, the call tree generated by applying the fibonacci function to the input 4.
This time, the anamorphism is the generation of the call tree isomorphic to the tree with leaf nodes 0, 1, 1, 0, 1 and the catamorphism the summation of these leaf nodes.
See also
References
- Erik Meijer, Maarten Fokkinga, Ross Paterson (1991). "Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire". pp. 4, 5. http://citeseer.ist.psu.edu/cachedpage/214108/1.