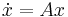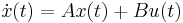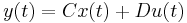Hurwitz matrix
Contents |
Hurwitz matrix and the Hurwitz stability criterion
In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficients of a real polynomial. Namely, given a real polynomial
the 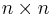 square matrix
square matrix
is called Hurwitz matrix corresponding to the polynomial  . It was established by Adolf Hurwitz in 1895 that a real polynomial is stable (that is, all its roots lie in the open left half-plane of the complex plane) if and only if all the leading principal minors of the matrix
. It was established by Adolf Hurwitz in 1895 that a real polynomial is stable (that is, all its roots lie in the open left half-plane of the complex plane) if and only if all the leading principal minors of the matrix 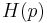 are positive:
are positive:
and so on. The minors 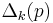 are called the Hurwitz determinants.
are called the Hurwitz determinants.
Hurwitz stable matrices
In engineering and stability theory, a square matrix  is called stable matrix (or sometimes Hurwitz matrix) if every eigenvalue of
is called stable matrix (or sometimes Hurwitz matrix) if every eigenvalue of  has strictly negative real part, that is,
has strictly negative real part, that is,
for each eigenvalue 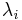 .
.  is also called a stability matrix, because then the differential equation
is also called a stability matrix, because then the differential equation
is asymptotically stable, that is, 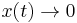 as
as 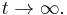 Hurwitz matrix is named after Adolf Hurwitz.
Hurwitz matrix is named after Adolf Hurwitz.
If 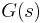 is a (matrix-valued) transfer function, then
is a (matrix-valued) transfer function, then  is called Hurwitz if the poles of all elements of
is called Hurwitz if the poles of all elements of  have negative real part. Note that it is not necessary that
have negative real part. Note that it is not necessary that 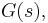 for a specific argument
for a specific argument 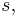 be a Hurwitz matrix — it need not even be square. The connection is that if
be a Hurwitz matrix — it need not even be square. The connection is that if  is a Hurwitz matrix, then the dynamical system
is a Hurwitz matrix, then the dynamical system
has a Hurwitz transfer function.
Any hyperbolic fixed point (or equilibrium point) of a continuous dynamical system is locally asymptotically stable if and only if the Jacobian of the dynamical system is Hurwitz stable at the fixed point.
The Hurwitz stability matrix is in crucial part on control theory. A system is stable if its control matrix is a Hurwitz matrix. The negative real components of the eigenvalues of the matrix represent negative feedback. Similarly, a system is inherently unstable if any of the eigenvalues have positive real components, representing positive feedback.
References
- Hurwitz, A. (1895). "Ueber die Bedingungen, unter welchen eine Gleichung nur Wurzeln mit negativen reellen Teilen besitzt". Mathematische Annalen Nr. 46, Leipzig: 273–284.
- Gantmacher, F.R. (1959). "Applications of the Theory of Matrices". Interscience, New York 641 (9): 1–8.
- Hassan K. Khalil (2002). Nonlinear Systems. Prentice Hall.
- Siegfried H. Lehnigk, On the Hurwitz matrix, Zeitschrift für Angewandte Mathematik und Physik (ZAMP), May 1970
- Bernard A. Asner, Jr., On the Total Nonnegativity of the Hurwitz Matrix, SIAM Journal on Applied Mathematics, Vol. 18, No. 2 (Mar., 1970)
- Dimitar K. Dimitrov and Juan Manuel Peña, Almost strict total positivity and a class of Hurwitz polynomials, Journal of Approximation Theory, Volume 132, Issue 2 (February 2005)
External links
This article incorporates material from Hurwitz matrix on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
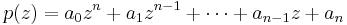

![\begin{align}
\Delta_1(p) &= \begin{vmatrix} a_{1} \end{vmatrix} &&=a_{1} > 0 \\[2mm]
\Delta_2(p) &= \begin{vmatrix}
a_{1} & a_{3} \\
a_{0} & a_{2} \\
\end{vmatrix} &&= a_2 a_1 - a_0 a_3 > 0\\[2mm]
\Delta_3(p) &= \begin{vmatrix}
a_{1} & a_{3} & a_{5} \\
a_{0} & a_{2} & a_{4} \\
0 & a_{1} & a_{3} \\
\end{vmatrix} &&= a_3 \Delta_2 - a_1 (a_1 a_4 - a_0 a_5 ) > 0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/fb2326940a1ad88b0781e047dc581a65.png)
![\mathop{\mathrm{Re}}[\lambda_i] < 0\,](/2012-wikipedia_en_all_nopic_01_2012/I/80385a6ca3c1c823309aa1805222e390.png)