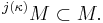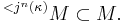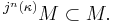Huge cardinal

In mathematics, a cardinal number κ is called huge if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and

Here, ^αM is the class of all sequences of length α whose elements are in M.

Huge cardinals were introduced by Kenneth Kunen (1978).

Contents 1 Variants 2 Consistency strength 3 ω-huge cardinals 4 See also 5 References

Variants

In what follows, jⁿ refers to the n-th iterate of the elementary embedding j, that is, j composed with itself n times, for a finite ordinal n. Also, ^<αM is the class of all sequences of length less than α whose elements are in M. Notice that for the "super" versions, γ should be less than j(κ), not .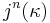

κ is almost n-huge if and only if there is j : V → M with critical point κ and

κ is super almost n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and

κ is n-huge if and only if there is j : V → M with critical point κ and

κ is super n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and

Notice that 0-huge is the same as measurable cardinal; and 1-huge is the same as huge. A cardinal satisfying one of the rank into rank axioms is n-huge for all finite n.

The existence of an almost huge cardinal implies that Vopenka's principle is consistent; more precisely any almost huge cardinal is also a Vopenka cardinal.

Consistency strength

The cardinals are arranged in order of increasing consistency strength as follows:

• almost n-huge
• super almost n-huge
• n-huge
• super n-huge
• almost n+1-huge

The consistency of a huge cardinal implies the consistency of a supercompact cardinal, nevertheless, the least huge cardinal is smaller than the least supercompact cardinal (assuming both exist).

ω-huge cardinals

One can try defining an ω-huge cardinal κ as one such that an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and ^λM⊆M, where λ is the supremum of jⁿκ for positive integers n. However Kunen's inconsistency theorem shows that ω-huge cardinals are inconsistent in ZFC, though it is still open whether they are consistent in ZF.

See also

• List of large cardinal properties
• The Dehornoy order on a braid group was motivated by properties of huge cardinals.

References

• Kunen, Kenneth (1978), "Saturated ideals", The Journal of Symbolic Logic 43 (1): 65–76, doi:10.2307/2271949, ISSN 0022-4812, MR495118 
• Penelope Maddy,"Believing the Axioms,II"(i.e. part 2 of 2),"Journal of Symbolic Logic",vol.53,no.3,Sept.1988,pages 736 to 764 (esp.754-756).
• Kanamori, Akihiro (2003). The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed ed.). Springer. ISBN 3-540-00384-3.