Hotelling's rule
Hotelling's rule states that the most socially and economically profitable extraction path of a non-renewable resource is one along which the price of the resource, determined by the marginal net revenue from the sale of the resource, increases at the rate of interest. It describes the time path of natural resource extraction which maximizes the value of the resource stock.[1]
This rule is derived from the work of a U.S. Economist Harold Hotelling in his seminal paper “The Economics of Exhaustible Resources” (Hotelling 1931), published in the Journal of Political Economy. This paper has laid the foundation for further research in the field of non-renewable resource economics.[1]
Contents |
History
During the late nineteenth and early twentieth century, the Conservation in the United States has been significantly visible. This Conservation Movement was concerned about the possible overexploitation of the non-renewable natural resources and called for a regulation. Harold Hotelling responded to this call with his seminal paper. In fact, he begins his paper with an introduction to this problem by stating that:[1]
- “Contemplation of the world’s disappearing supplies of minerals, forests, and other exhaustible assets had led to demands for regulation of their exploitation. The feeling that these products are now too cheap for the good of future generations, that they are being selfishly exploited at too rapid a rate, and that in consequence of their excessive cheapness they are being produced and consumed wastefully has given rise to the conservation movement.” - Harold Hotelling (1931)[2]
Before 1970s serious attention was not given to Hotelling’s views regarding economics of exhaustible resources. This was due to the fact that when Hotelling came up with this hypothesis, the media’s emphasis was towards issues like the Great Depression and the World War of the 1940s.
After World War II, there were concerns about the sufficiency and adequacy of natural resources especially in the US. This led to the establishment of the President’s Materials Policy Commission, called the Paley commission, the report of which was published in 1952. It was an outcome of the Resources of the Future, a part of the Washington think tank. However this did not help in any way in recognizing Hotelling’s work. In 1963, Harold Barnett and Chandler Morse published their paper, Scarcity and Growth, which was one of the first of its kinds in analysing the long run measures of scarcity of a number of natural resources in a systematic fashion. A passing reference to Hotelling’s paper was made in that paper. This takes us to the conclusion that a lack of attention and interest to Hotelling’s work cannot be attributed to the lack of public concern for the issues relating natural resources before 1970s as there is no sufficient evidence to prove this point.
Hotelling’s paper was difficult and given the level of sophistication in economic profession concerning mathematics at that time, it might have been a reason why his contribution got unnoticed. In fact Hotelling himself stated that the Economic Journal had rejected his paper due to high difficulty level of mathematics involved in it.
The publication by Dennis Meadows et al. The Limits to Growth in the year 1972 set off another period of intense public concern for natural resources. According to the publication unless economic growth was cut back, there would be disastrous consequences on the level of natural resources. This made Hotelling rule, which consisted of optimal control theory, seek attention from the academic economists. In 1973 “The Allocation of Energy Resources“ was published by William Nordhaus. It was a vital piece of study which sought to solve the problem of usage of different energy resources by applying the Hotelling model. Nordhaus also published in the next year a critical analysis of The Limits to Growth in American Economic Review. The subject of natural resource economics got further contribution from Robert Solow who committed his 1974 Ely Lecture to the American Economic Association. In the same year Partha Dasgupta, Geoffrey Heal, Tjalling Koopmans, Joseph Stiglitz and Robert Solow contributed to the topic of exhaustible resources which was published by Review of Economic Studies. All these events provided greater weight and prominence to Natural resource economics as a field of research. The now famous Hotelling’s rule acquired the centre stage and still continues to maintain its position.[1]
The Rule
As mentioned earlier, and in Jeffrey A. Krautkraemer’s words, “Hotelling’s formal analysis of nonrenewable resource depletion generates some basic implications for how the finite availability of a nonrenewable resource affects the resource price and extraction paths.”[2]
Hotelling’s rule primarily addresses one basic question of the owner or agent involved in the exploitation of the non-renewable resource: How much of the asset should I consume now and how much should I store for the future? In other words, the agent has to choose between the current value of the asset if extracted and sold and the future increased value of the asset if left unexploited. This simple rule can be expressed by the equilibrium situation representing the optimal solution.
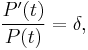
when P(t) is the unit profit at time t and δ is the discount rate(the inverse of rate of return).
The stock of a non-renewable resource, being an asset, holds a market value which yields returns to its owner at a certain rate. This rate of return can be determined by three components:
- Flow of product generated by the marginal unit of the resource, Marginal Productivity or Dividend rate.
- Change in the physical characteristics of the asset over time.
- The rate at which market value of the asset will change over time.
The equality of this rate of return to the rate of return of alternative investments (i.e. if the yield obtained from asset’s sale is invested elsewhere) determines the asset market’s equilibrium. Considering a nonrenewable resource, say a stock of oil in the ground, which is subject to two characteristics; one, it has a fixed size which cannot be increased over time and two, the in-situ asset is unproductive. This makes the first component, marginal productivity nil. Assuming that holding the asset in-situ will not lead to its depreciation, even the second component is rendered zero. Remainder is the rate of appreciation of the asset’s value which is hence, the only determinant of rate of return of the stock of oil.[1]
Framework
The value of the marginal unit of the natural resource held in-situ less the cost of taking it out of the ground is what its value of the resource would be in the flow market. If p(t) is the price which the extracted resource can fetch on the market and c(t) is the marginal cost of extracting it at date t, then its marginal value must be:
Π(t) = p(t) − c(t),
which represents the asset price of the resource. . Denoting the rate of interest by r, then asset markets equilibrium is established when
Π'(t)/ Π(t)= r
This is the famous Hotelling’s rule which states the asset market equilibrium condition. It states that the net price of the natural resource must grow at the rate of interest.
Assuming that the marginal cost of extracting the resource does not depend on the rate of extraction and doest not vary over time, then the market price of the asset over time would be
p'(t)/ p(t)= r (1 - c/ p(t))
If this was the case then the rate of growth of the observed price of non-renewable resource would be inclined towards the rate of interest as the proportion of costs in price gets smaller and the rent brought about by the scarcity of the natural resource gets higher.
But this is not in line with the statistics observed over more than a century. Statistics concerning U.S. price data for the period 1870-2004 for copper, lead, zinc, coal and petroleum, 1880-2004 for tin, 1900-2004 for aluminium and nickel and 1920-2004 for natural gas, reveal the rate of change of prices of these resources being influenced by a high degree of volatility. But the more important phenomena is that the volatility seemed to be centered at 0. In fact the mean rate of change of price in none of the ten cases is considerably different from 0. Thus the actual price of the resources does not seem to be following a particular trend and definitely not the path of the positive trend as recommended by Hotelling’s Rule.[1]
Drawback
While the rule predicts an exponentially increasing resource prices, the results of the empirical studies are not in tandem with the rule. The results so far showed either declining or constant resource prices over time. In response to this contrast, many economists and researchers tried to bridge this gap by plugging in more variables to see their influence on resource price. Alternatively, some authors tried using different econometric techniques to generate rising data on resource prices.[3]
References
- ^ a b c d e f Gaudet, Gérard (June 2007). Natural Resource Economics under the Rule of Hotelling. http://www.middleeastoil.net/Natural%20Resource%20Economics%20under%20the%20Rule%20of%20Hotelling1.pdf.
- ^ a b Krautkraemer, Jeffrey A.. Journal of Economic Literature. http://msuweb.montclair.edu/~lebelp/JKrautkramerNonRenResScarcityJEL1998.pdf.
- ^ The Hotelling’s Rule Revisited in a Dynamic General Equilibrium Model. https://ioes.hi.is/events/DEGIT_IX/Papers/Yetkiner_Gaitan.pdf.