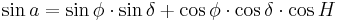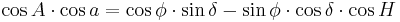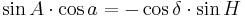Horizontal coordinate system

The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane. This coordinate system divides the sky into the upper hemisphere where objects are visible, and the lower hemisphere where objects cannot be seen since the earth is in the way. The pole of the upper hemisphere is called the zenith. The pole of the lower hemisphere is called the nadir. ^[1]

The horizontal coordinates are:

Altitude (Alt), sometimes referred to as elevation, is the angle between the object and the observer's local horizon. It is expressed as an angle between 0 degrees to 90 degrees.
Azimuth (Az), that is the angle of the object around the horizon, usually measured from the north increasing towards the east.
Zenith distance, the distance from directly overhead (i.e. the zenith) is sometimes used instead of altitude in some calculations using these coordinates. The zenith distance is the complement of altitude (i.e. 90°-altitude).

The horizontal coordinate system is sometimes also called the az/el^[2] or Alt/Az coordinate system.

1 General observations
2 Transformation of coordinates
- 2.1 equatorial to horizontal
- 2.2 horizontal to equatorial
3 The position of the Sun
4 See also
5 References

General observations

The horizontal coordinate system is fixed to the Earth, not the stars. Therefore, the altitude and azimuth of an object changes with time, as the object appears to drift across the sky. In addition, because the horizontal system is defined by the observer's local horizon, the same object viewed from different locations on Earth at the same time will have different values of altitude and azimuth.

Horizontal coordinates are very useful for determining the rise and set times of an object in the sky. When an object's altitude is 0°, it is on the horizon. If at that moment its altitude is increasing, it is rising, but if its altitude is decreasing it is setting. However, all objects on the celestial sphere are subject to diurnal motion, which is always from east to west. One can determine whether altitude is increasing or decreasing by instead considering the azimuth of the celestial object:

if the azimuth is between 0° and 180° (north–east–south), it is rising.
if the azimuth is between 180° and 360° (south–west–north), it is setting.

There are the following special cases:

At the north pole all directions are south, and at the south pole all directions are north, so the azimuth is undefined in both locations. A star (or any object with fixed equatorial coordinates) has constant altitude, and therefore never rises or sets when viewed from either pole. The Sun, Moon, and planets can rise or set over the span of a year when viewed from the poles because their right ascensions and declinations are constantly changing.
At the equator objects on the celestial poles stay at fixed points on the horizon.

Note that the above considerations are strictly speaking true for the geometric horizon only: the horizon as it would appear for an observer at sea level on a perfectly smooth Earth without an atmosphere. In practice the apparent horizon has a negative altitude, whose absolute value gets larger as the observer ascends higher above sea level, due to the curvature of the Earth. In addition, atmospheric refraction causes celestial objects very close to the horizon to appear about half a degree higher than they would if there were no atmosphere.

Transformation of coordinates

It is possible to convert from the equatorial coordinate system to the horizontal coordinate system and back. Define variables as follows:

φ = geographic latitude
A = azimuth
a = altitude
δ = declination
H = hour angle

equatorial to horizontal

The following procedure allows conversion of equatorial coordinates to horizontal coordinates.^[3]

$\sin a = \sin \phi \cdot \sin \delta %2B \cos \phi \cdot \cos \delta \cdot \cos H$

$\cos A \cdot \cos a = \cos \phi \cdot \sin \delta - \sin \phi \cdot \cos \delta \cdot \cos H$

$\sin A \cdot \cos a = - \cos \delta \cdot \sin H$

One may be tempted to simplify the last two equations by dividing out the cos a term, leaving one expression in tan A only. But the tangent cannot distinguish between (for example) an azimuth of 45° and 225°. These two values are very different: they are opposite directions, NE and SW respectively. One can do this only when the quadrant in which the azimuth lies is already known.

If the calculation is done with an electronic pocket calculator, it is best not to use the functions arcsin and arccos when possible, because of their limited 180° only range, and also because of the low accuracy the former gets around ±90° and the latter around 0° and 180°. Most scientific calculators have a rectangular to polar (R→P) and polar to rectangular (P→R) function, which avoids that problem and gives us an extra sanity check as well.

The algorithm then becomes as follows.

Calculate the right hand side of the three equations given above.
Apply a R→P conversion taking X = cos A cos a, and Y = sin A cos a.
The angle part of the answer is the azimuth.
Apply a second R→P conversion taking the radius part of the last answer as the X and the sin a of the first equation as the Y value.
The angle part of the answer is the altitude, an angle between −90° and +90°.
The radius part of the answer must be 1 exactly, or you have made an error.

horizontal to equatorial

$\sin \delta = \sin \phi \cdot \sin a %2B \cos \phi \cdot \cos a \cdot \cos A$

$\cos \delta \cdot \cos H = \cos \phi \cdot \sin a - \sin \phi \cdot \cos a \cdot \cos A$

$\cos \delta \cdot \sin H = -\sin A \cdot \cos a$

The same quadrant considerations from the first set of formulas also hold for this set.

The position of the Sun

There are several ways to compute the apparent position of the Sun in horizontal coordinates.

Complete and accurate algorithms to obtain precise values can be found in Jean Meeus's book Astronomical Algorithms.

Instead a simple approximate algorithm is the following:

Given:

the date of the year and the time of the day
the observer's latitude, longitude and time zone

You have to compute:

The Sun declination of the corresponding day of the year, which is given by the following formula which has less than 2 degrees of error:

$\delta = -23.45^\circ \cdot \cos \left ( \frac{360^\circ}{365} \cdot \left ( N %2B 10 \right ) \right )$

where $N$ is the number of days spent since January 1.

The true hour angle that is the angle which the earth should rotate to take the observer's location directly under the sun.
- Let hh:mm be the time the observer reads on the clock.
- Merge the hours and the minutes in one variable $T$ = hh + mm/60 measured in hours.
- hh:mm is the official time of the time zone, but it is different from the true local time of the observer's location. $T$ has to be corrected adding the quantity + (Longitude/15 – Time Zone), which is measured in hours and represents the difference of time between the true local time of the observer's location and the official time of the time zone.
- If it is summer and Daylight Saving Time is used, you have to subtract one hour in order to get Standard Time.
- The value of the Equation of Time in that day has to be added. Since $T$ is measured in hours, the Equation of Time must be divided by 60 before being added.
- The hour angle can be now computed. In fact the angle which the earth should rotate to take the observer's location directly under the sun is given by the following expression: $H$ = (12 – $T$ ) * 15. Since $T$ is measured in hours and the speed of rotation of the earth 15 degrees per hour, $H$ is measured in degrees. If you need $H$ measured in radians you just have to multiply by the factor 2π/360.

Use the Transformation of Coordinates to compute the apparent position of the Sun in horizontal coordinates.

References

^ Schombert, James. "Earth Coordinate System". University of Oregon Department of Physics. http://abyss.uoregon.edu/~js/ast121/lectures/lec03.html. Retrieved 19 March 2011.
^ hawaii.edu
^ Oliver Montenbruck and Thomas Pfleger. Astronomy on the Personal Computer. Springer-Verlag. p. 37. ISBN 0-387-57700-9.

Celestial coordinate systems

Horizontal coordinate system · Equatorial coordinate system · Ecliptic coordinate system · Galactic coordinate system · Supergalactic coordinate system

See also: Coordinate system · Converting coordinates