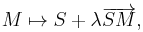Homothetic transformation
In mathematics, a homothety (or homothecy or dilation) is a transformation of an affine space determined by a point S called its center and a nonzero number λ called its ratio, which sends
in other words it fixes S, and sends any M to another point N such that the segment SN is on the same line as SM, but scaled by a factor λ.[1] In Euclidean geometry homotheties are the similarities that fix a point and either preserve (if λ > 0) or reverse (if λ < 0) the direction of all vectors. Together with the translations, all homotheties of an affine (or Euclidean) space form a group, the group of homothety-translations. These are precisely the affine transformations with the property that the image of every line L is a line parallel to L.
In Euclidean geometry, a homothety of ratio λ multiplies distances between points by |λ| and all areas by λ2. The first number is called the ratio of magnification or dilation factor or scale factor or similitude ratio. Such a transformation can be called an enlargement if the scale factor exceeds 1.
See also
- Scaling (geometry) a similar notion in vector spaces
- Homothetic center, the center of a homothetic transformation taking one of a pair of shapes into the other
- The Hadwiger conjecture on the number of strictly smaller homothetic copies of a convex body that may be needed to cover it
- Homothetic function (economics), a function of the form U(f(y)) in which f is a homogeneous function and U is a monotonically increasing function.
References
- ^ J. Hadamard, Lessons in Plane Geometry, p. 145
External links
- Homothety, interactive applet from Cut-the-Knot.