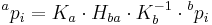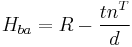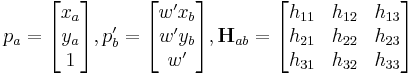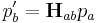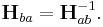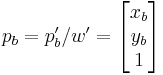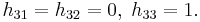Homography

For the concept in linguistics also called homography, see heterography and homography.

Homography is a concept in the mathematical science of geometry. A homography is an invertible transformation from a projective space (for example, the real projective plane) to itself that maps straight lines to straight lines. Synonyms are collineation, projective transformation, and projectivity,[1] though "collineation" is also used more generally.

Formally, a projective transformation in a plane is a transformation used in projective geometry: it is the composition of a pair of perspective projections. It describes what happens to the perceived positions of observed objects when the point of view of the observer changes. Projective transformations do not preserve sizes or angles but do preserve incidence and cross-ratio: two properties which are important in projective geometry. Projectivities form a group.[1]

For more general projective spaces – of different dimensions or over different fields – "homography" means a projective linear transformation (an invertible transformation induced by a linear transformation of the associated vector space), while "collineation" (meaning "maps lines to lines") is more general, and includes both homographies and automorphic collineations (collineations induced by a field automorphism), as well as combinations of these.

Contents

Computer vision applications

In the field of computer vision, any two images of the same planar surface in space are related by a homography (assuming a pinhole camera model). This has many practical applications, such as image rectification, image registration, or computation of camera motion—rotation and translation—between two images. Once camera rotation and translation have been extracted from an estimated homography matrix, this information may be used for navigation, or to insert models of 3D objects into an image or video, so that they are rendered with the correct perspective and appear to have been part of the original scene (see Augmented Reality).

3D plane to plane equation

We have two cameras a and b, looking at points 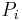P_i in a plane.

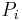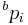Passing the projections of P_i from {}^bp_i in b to a point 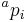{}^ap_i in a:

{}^ap_i = K_a \cdot H_{ba} \cdot K_b^{-1} \cdot {}^bp_i

where H_{ba} is

H_{ba} = R - \frac{t n^T}{d}

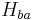R is the rotation matrix by which b is rotated in relation to a; t is the translation vector from a to b; n and d are the normal vector of the plane and the distance to the plane respectively.

Ka and Kb are the cameras' intrinsic parameter matrices.

The figure shows camera b looking at the plane at distance d.

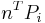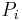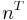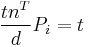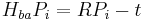Note: From above figure, n^T P_i is the projection of vector P_i into n^T, and equal to d. So \frac{t n^T}{d} P_i = t. And we have H_{ba} P_i = R P_i - t.

Mathematical definition

In the complex plane, a Mobius transformation is frequently called a homography. These linear-fractional transformations are expressions of projective transformations on the complex projective line, an extension of the complex plane.

In higher dimensions Homogeneous coordinates are used to represent projective transformations by means of matrix multiplications. With Cartesian coordinates matrix multiplication cannot perform the division required for perspective projection. In other words, with Cartesian coordinates a perspective projection is a non-linear transformation.

Given:

p_a = \begin{bmatrix} x_a\\y_a\\1\end{bmatrix}, p^\prime_b = \begin{bmatrix} w^{\prime}x_b\\w^{\prime}y_{b}\\w^{\prime}\end{bmatrix}, \mathbf{H}_{ab} = \begin{bmatrix} h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33} \end{bmatrix}

Then:

p^\prime_b = \mathbf{H}_{ab}p_a \,

where:

\mathbf{H}_{ba} = \mathbf{H}_{ab}^{-1}.

Also:

p_b = p^\prime_b/w^\prime = \begin{bmatrix} x_b\\y_b\\ 1\end{bmatrix}

Affine homography

When the image region in which the homography is computed is small or the image has been acquired with a large focal length, an affine homography is a more appropriate model of image displacements. An affine homography is a special type of a general homography whose last row is fixed to

h_{31}=h_{32}=0, \; h_{33}=1.

See also

References

  1. ^ a b Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press. pp. 32–33. ISBN 0-521-54051-8. 

External links