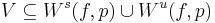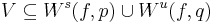Homoclinic connection
In dynamical systems, a branch of mathematics, a structure formed from the stable manifold and unstable manifold of a fixed point.
Contents |
Definition for maps
Let 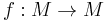 be a map defined on a manifold
be a map defined on a manifold  , with a fixed point
, with a fixed point  . Let
. Let 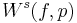 and
and 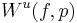 be the stable manifold and the unstable manifold of the fixed point
be the stable manifold and the unstable manifold of the fixed point  , respectively. Let
, respectively. Let  be an connected invariant manifold such that
be an connected invariant manifold such that
Then  is called a homoclinic connection.
is called a homoclinic connection.
Heteroclinic connection
It is a similar notion, but it refers to two fixed points,  and
and  . The condition satisfied by
. The condition satisfied by  is replaced with:
is replaced with:
This notion is not symmetric with respect to  and
and  .
.
Homoclinic and heteroclinic intersections
When the invariant manifolds 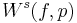 and
and 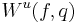 , possibly with
, possibly with 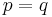 , intersect but there is no homoclinic/heteroclinic connection, a different structure is formed by the two manifolds, sometimes referred to as the homoclinic/heteroclinic tangle. The figure has a conceptual drawing illustrating their complicated structure. The theoretical result supporting the drawing is the lambda-lemma. Homoclinic tangles are always accompanied by a Smale horseshoe.
, intersect but there is no homoclinic/heteroclinic connection, a different structure is formed by the two manifolds, sometimes referred to as the homoclinic/heteroclinic tangle. The figure has a conceptual drawing illustrating their complicated structure. The theoretical result supporting the drawing is the lambda-lemma. Homoclinic tangles are always accompanied by a Smale horseshoe.
Definition for continuous flows
For continuous flows, the definition is essentially the same.
Comments
- There is some variation in the definition across various publications;
- Historically, the first case considered was that of a continuous flow on the plane, induced by an ordinary differential equation. In this case, a homoclinic connection is a single trajectory that converges to the fixed point
 both forwards and backwards in time. A pendulum in the absence of friction is an example of a mechanical system that does have a homoclinic connection. When the pendulum is released from a the top position (the point of highest potential energy), with infinitesimally small velocity, the pendulum will return to the same position. Upon return, it will have exactly the same velocity. The time it will take to return will increase to
both forwards and backwards in time. A pendulum in the absence of friction is an example of a mechanical system that does have a homoclinic connection. When the pendulum is released from a the top position (the point of highest potential energy), with infinitesimally small velocity, the pendulum will return to the same position. Upon return, it will have exactly the same velocity. The time it will take to return will increase to 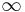 as the initial velocity goes to zero. One of the demonstrations in the pendulum article exhibits this behavior.
as the initial velocity goes to zero. One of the demonstrations in the pendulum article exhibits this behavior.
Significance
When a dynamical system is perturbed, a homoclinic connection splits. It becomes a disconnected invariant set. Near it, there will be a chaotic set called Smale's horseshoe. Thus, the existence of a homoclinic connection is thus considered as potentially leading to chaos. For example, when a pendulum is placed in a box, and the box is subjected to small horizontal oscillations, the pendulum may exhibit chaotic behavior.