Hom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
Contents |
Formal definition
Let C be a locally small category (i.e. a category for which hom-classes are actually sets and not proper classes).
For all objects A and B in C we define two functors to the category of sets as follows:
| Hom(A,–) : C → Set | Hom(–,B) : C → Set |
|---|---|
| This is a covariant functor given by: | This is a contravariant functor given by: |
The functor Hom(–,B) is also called the functor of points of the object B.
Note that fixing the first argument of Hom naturally gives rise to a covariant functor and fixing the second argument naturally gives a contravariant functor. This is an artifact of the way in which one must compose the morphisms.
The pair of functors Hom(A,–) and Hom(–,B) are obviously related in a natural manner. For any pair of morphisms f : B → B′ and h : A′ → A the following diagram commutes:
Both paths send g : A → B to f ∘ g ∘ h.
The commutativity of the above diagram implies that Hom(–,–) is a bifunctor from C × C to Set which is contravariant in the first argument and covariant in the second. Equivalently, we may say that Hom(–,–) is a covariant bifunctor
- Hom(–,–) : Cop × C → Set
where Cop is the opposite category to C.
Yoneda's lemma
Referring to the above commutative diagram, one observes that every morphism
- h : A′ → A
gives rise to a natural transformation
- Hom(h,–) : Hom(A,–) → Hom(A′,–)
and every morphism
- f : B → B′
gives rise to a natural transformation
- Hom(–,f) : Hom(–,B) → Hom(–,B′)
Yoneda's lemma implies that every natural transformation between Hom functors is of this form. In other words, the Hom functors give rise to a full and faithful embedding of the category C into the functor category SetC (covariant or contravariant depending on which Hom functor is used).
Other properties
If A is an abelian category and A is an object of A, then HomA(A,–) is a covariant left-exact functor from A to the category Ab of abelian groups. It is exact if and only if A is projective.[1]
Let R be a ring and M a left R-module. The functor HomZ(M,–): Ab → Mod-R is right adjoint to the tensor product functor –  R M: Mod-R → Ab.
R M: Mod-R → Ab.
See also
Notes
- ^ Jacobson (2009), p. 149, Prop. 3.9.
References
- Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (Second ed.). Springer. ISBN 0-387-98403-8.
- Goldblatt, Robert (2006) [1984]. Topoi, the Categorial Analysis of Logic (Revised ed.). Dover Publications. ISBN 978-0486450261. http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=Gold010&id=3. Retrieved 2009-11-25.
- Jacobson, Nathan (2009). Basic algebra. 2 (2nd ed.). Dover. ISBN 978-0-486-47187-7.
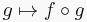 for each g in Hom(A, X).
for each g in Hom(A, X).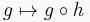 for each g in Hom(Y, B).
for each g in Hom(Y, B).