Hoffman–Singleton graph

Hoffman–Singleton graph

Named after	Alan J. Hoffman Robert R. Singleton
Vertices	50
Edges	175
Radius	2
Diameter	2^[1]
Girth	5^[1]
Automorphisms	252,000 (PSU(3,5²):2)^[2]
Chromatic number	4
Chromatic index	7^[3]
Properties	Strongly regular Symmetric Hamiltonian Integral Cage Moore graph Cayley graph

In the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters (50,7,0,1).^[4] It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is the highest order Moore graph known to exist.^[5] Since it is a Moore graph where each vertex has degree 7, and the girth is 5, it is a (7,5)-cage.

1 Construction
2 Algebraic properties
3 Subgraphs
4 See also
5 Notes
6 References

Construction

A simple direct construction is the following: Take five pentagons P_h and five pentagrams Q_i, so that vertex j of P_h is adjacent to vertices j-1,j+1 of P_h and vertex j of Q_i is adjacent to vertices j-2,j+2 of Q_i. Now join vertex j of P_h to vertex hi+j of Q_i. (All indices mod 5.)

Algebraic properties

The automorphism group of the Hoffman-Singleton graph is a group of order 252,000 isomorphic to PΣU(3,5²) the semidirect product of the projective special unitary group PSU(3,5²) with the cyclic group of order 2 generated by the Frobenius automorphism. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Hoffman-Singleton graph is a symmetric graph. It is also a Cayley graph.

The characteristic polynomial of the Hoffman-Singleton graph is equal to 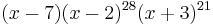$(x-7) (x-2)^{28} (x%2B3)^{21}$ . Therefore the Hoffman-Singleton graph is an integral graph: its spectrum consists entirely of integers.

Subgraphs

Using only the fact that the Hoffman-Singleton graph is a strongly regular graph with parameters (50,7,0,1), it can be shown that there are 1260 5-cycles contained in the Hoffman-Singleton graph.

Additionally, the Hoffman-Singleton graph contains 525 copies of the Petersen graph.

Notes

^ ^a ^b Weisstein, Eric W., "Hoffman-Singleton Graph" from MathWorld.
^ Hafner, P. R. "The Hoffman-Singleton Graph and Its Automorphisms." J. Algebraic Combin. 18, 7-12, 2003.
^ Royle, G. "Re: What is the Edge Chromatic Number of Hoffman-Singleton?" GRAPHNET@istserv.nodak.edu posting. Sept. 28, 2004. [1]
^ Brouwer, Andries E., Hoffman-Singleton graph, http://www.win.tue.nl/~aeb/drg/graphs/Hoffman-Singleton.html .
^ Hoffman, Alan J.; Singleton, Robert R. (1960), "Moore graphs with diameter 2 and 3", IBM Journal of Research and Development 5 (4): 497–504, MR 0140437, http://www.research.ibm.com/journal/rd/045/ibmrd0405H.pdf .

References

Benson, C. T.; Losey, N. E. (1971), "On a graph of Hoffman and Singleton", Journal of Combinatorial Theory. Series B 11 (1): 67–79, doi:10.1016/0095-8956(71)90015-3, ISSN 0095-8956, MR 0281658
Holton, D.A.; Sheehan, J. (1993), The Petersen graph, Cambridge University Press, pp. 186 and 190, ISBN 0-521-43594-3 .