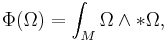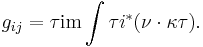Hitchin functional

The Hitchin functional is a mathematical concept with applications in string theory that was introduced by the British mathematician Nigel Hitchin.^[1]

As with Hitchin's introduction of generalized complex manifolds, this is an example of a mathematical tool found useful in theoretical physics.

1 Formal definition
2 Properties
3 Use in string theory
4 Notes

Formal definition

This is the definition for 6-manifolds. The definition in Hitchin's article is more general, but more abstract.

Let $M$ be a compact, oriented 6-manifold with trivial canonical bundle. Then the Hitchin functional is a functional on 3-forms defined by the formula:

$\Phi(\Omega) = \int_M \Omega \wedge * \Omega,$

where $\Omega$ is a 3-form and * denotes the Hodge star operator.

Properties

The Hitchin functional is analogous to the Yang-Mills functional for the four-manifolds.

The Hitchin functional is manifestly invariant under the action of the group of orientation-preserving diffeomorphisms.

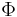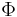Theorem. Suppose that $M$ is a three-dimensional complex manifold and $\Omega$ is the real part of a non-vanishing holomorphic 3-form, then $\Omega$ is a critical point of the functional $\Phi$ restricted to the cohomology class $[\Omega] \in H^3(M,R)$ . Conversely, if $\Omega$ is a critical point of the functional $\Phi$ in a given comohology class and 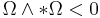$\Omega \wedge * \Omega < 0$ , then $\Omega$ defines the structure of a complex manifold, such that $\Omega$ is the real part of a non-vanishing holomorphic 3-form on $M$ .

The proof of the theorem in Hitchin's article ^[1] is relatively straightforward. The power of this concept is in the converse statement: if the exact form 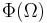$\Phi(\Omega)$ is known, we only have to look at its critical points to find the possible complex structures.

Use in string theory

Hitchin functionals arise in many areas of string theory. An example is the compactifications of the 10-dimensional string with a subsequent orientifold projection $\kappa$ using an involution $\nu$ . In this case, $M$ is the internal 6 (real) dimensional Calabi-Yau space. The couplings to the complexified Kähler coordinates $\tau$ is given by

$g_{ij} = \tau \text{im} \int \tau i^*(\nu \cdot \kappa \tau).$

The potential function is the functional $V[J] = \int J \wedge J \wedge J$ , where J is the almost complex structure. Both are Hitchin functionals.^[2]

Notes

^ ^a ^b The original article by Hitchin http://arxiv.org/abs/math/0010054
^ Hitchin functional in orientifold projections http://arxiv.org/abs/hep-th/0412277

Hitchin functional

Contents

Formal definition

Properties

Use in string theory

Notes