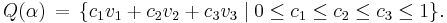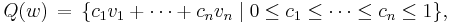Hill tetrahedron
In geometry, the Hill tetrahedra are a family of space-filling tetrahedra. They were discovered in 1896 by M.J.M. Hill, a professor of mathematics at the University College London, who showed that they are scissor-congruent to a cube.
Contents |
Construction
For every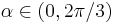 
, let 
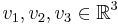be three unit vectors with angle 
between every two of them. Define the Hill tetrahedron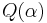 
as follows:
A special case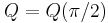 
is the tetrahedron having all sides right triangles with sides 1, 
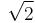and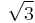 
. Ludwig Schläfli studied 
as a special case of the orthoscheme, and H.S.M. Coxeter called it the characteristic tetrahedron of the cubic spacefilling.
Properties
- A cube can be tiled with 6 copies of .
- Every 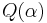can be dissected into three polytopes which can be reassembled into a prism.
Generalizations
In 1951 Hugo Hadwiger found the following n-dimensional generalization of Hill tetrahedra:
where vectors 
satisfy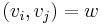 
for all 
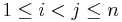, and where 
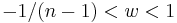. Hadwiger showed that all such simplices are scissor congruent to a hypercube.
References
- M. J. M. Hill, Determination of the volumes of certain species of tetrahedra without employment of the method of limits, Proc. London Math. Soc., 27 (1895–1896), 39–53.
- H. Hadwiger, Hillsche Hypertetraeder, Gazeta Matemática (Lisboa), 12 (No. 50, 1951), 47–48.
- H.S.M. Coxeter, Frieze patterns, Acta Arithmetica 18 (1971), 297–310.
- E. Hertel, Zwei Kennzeichnungen der Hillschen Tetraeder, J. Geom. 71 (2001), no. 1–2, 68–77.
- Greg N. Frederickson, Dissections: Plane and Fancy, Cambridge University Press, 2003.
- N.J.A. Sloane, V.A. Vaishampayan, Generalizations of Schobi’s Tetrahedral Dissection, arXiv:0710.3857.