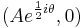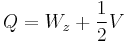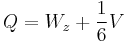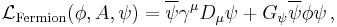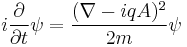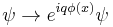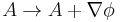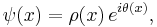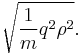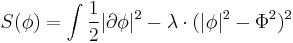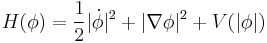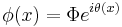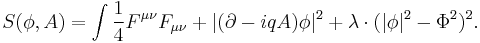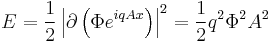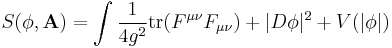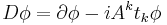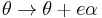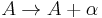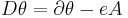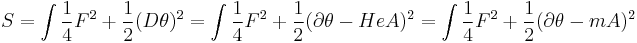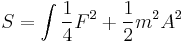Higgs mechanism

For Higgs fields in mathematics, see Higgs bundle.
Quantum field theory
History of...

In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking.

The simplest implementation of the mechanism adds an extra Higgs field to the gauge theory. The spontaneous symmetry breaking of the underlying local symmetry triggers conversion of components of this Higgs field to Goldstone bosons which interact with (at least some of) the other fields in the theory, so as to produce mass terms for (at least some of) the gauge bosons. This mechanism may also leave behind elementary scalar (spin-0) particles, known as Higgs bosons.

In the standard model, the phrase "Higgs mechanism" refers specifically to the generation of masses for the W±, and Z weak gauge bosons through electroweak symmetry breaking.[1] Although the evidence for the electroweak Higgs mechanism is overwhelming, experiments have yet to discover the single Higgs boson predicted by the standard model. The Large Hadron Collider at CERN is currently searching for Higgs bosons, and attempting to understand the electroweak Higgs mechanism.

The mechanism was proposed in 1962 by Philip Warren Anderson. The relativistic model was developed in 1964 by three independent groups: Robert Brout and Francois Englert; Peter Higgs; and Gerald Guralnik, C. R. Hagen, and Tom Kibble.

Contents

In the standard model

The Higgs mechanism was incorporated into modern particle physics by Steven Weinberg and Abdus Salam, and is an essential part of the standard model.

In the standard model, at temperatures high enough so that electroweak symmetry is unbroken, all elementary particles are massless. At a critical temperature, the symmetry is spontaneously broken, and the W and Z bosons acquire masses. (EWSB, ElectroWeak Symmetry Breaking, is an abbreviation used for this.)

Fermions, such as the leptons and quarks in the Standard Model, can also acquire mass as a result of their interaction with the Higgs field, but not in the same way as the gauge bosons.

Structure of the Higgs field

In the standard model, the Higgs field is an SU(2) doublet, a complex spinor with four real components (or equivalently with two complex components), with a Standard Model U(1) charge of −1.

It transforms as a spinor under SU(2). Under U(1) rotations, it gets multiplied by a phase; this mixes the real and imaginary part of the complex spinor into each other, so this is not the same as two complex spinors mixing under U(1) (which would have eight real components between them), but instead is the spinor representation of the group U(2).

The Higgs field, through the interactions specified by its potential, induces spontaneous breaking of three out of the four generators ("directions") of the gauge group SU(2)×U(1), and three out of its four components would ordinarily amount to Goldstone bosons, if they were not coupled to gauge fields. However, after symmetry breaking, these three of the four degrees of freedom in the Higgs field mix with the W and Z bosons, while the one remaining degree of freedom becomes the Higgs boson – a new scalar particle.

The part that remains massless

The gauge group of the electroweak part of the standard model is SU(2) × U(1).

The group SU(2) is all unitary matrices, all the orthonormal changes of coordinates in a complex two dimensional vector space. Rotating the coordinates so that the first basis vector points in the direction of H makes the vacuum expectation value of H the spinor (A, 0). The generators for rotations about the x, y, and z axes are by half the Pauli matrices \sigma_x, \sigma_y, \sigma_z, so that a rotation of angle θ about the z-axis takes the vacuum to:

(A e^{\frac{1}{2}i\theta},0)\,

While the X and Y generators mix up the top and bottom components of the spinor, the Z rotations only multiply by a phase. This phase can be undone by a U(1) rotation of angle ½θ, which multiplies by the opposite phase, since the Higgs has charge −1. Under both an SU(2) z-rotation and a U(1) rotation by an amount ½θ, the vacuum is invariant. This combination of generators:

Q = W_z %2B \frac{1}{2}V

defines the unbroken gauge group, where Wz is the generator of rotations around the z-axis in the SU(2) and V is the generator of the U(1). This combination of generators (a z rotation in the SU(2) and a simultaneous U(1) rotation by half the angle) preserves the vacuum, and defines the unbroken gauge group in the standard model. The part of the gauge field in this direction stays massless, and this gauge field is the actual photon.

The phase that a field acquires under this combination of generators is its electric charge, and this is the formula for the electric charge in the standard model. In this convention, all the V charges in the standard model are multiples of ⅓. To make all the V-charges in the standard model integers, you can rescale the V part of the formula by tripling all the V-charges if you like, and rewrite the charge formula as:

Q = W_z %2B \frac{1}{6}V

but the normalization with ½V is the universal standard.

Consequences for fermions

In spite of the introduction of spontaneous symmetry-breaking, also for fermions the mass terms oppose the chiral gauge invariance. Therefore, also for these fields the mass terms should be replaced by a gauge-invariant "Higgs" mechanism. An obvious possibility is some kind of "Yukawa coupling" (see below) between the fermion field ψ and the Higgs field Φ, with unknown couplings G_{\psi}, which after symmetry-breaking (more precisely: after expansion of the Lagrange density around a suitable ground state) again results in the original mass terms, which are now, however (i.e. by introduction of the Higgs field) written in a gauge-invariant way. The Lagrange density for the "Yukawa"-interaction of a fermion field 'ψ' and the Higgs field 'Φ' is

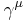\mathcal{L}_{\mathrm{Fermion}}(\phi , A, \psi ) = \overline{\psi} \gamma^{\mu} D_{\mu} \psi %2B G_{\psi} \overline{\psi} \phi \psi \,,

where again the gauge field A only enters D_\mu (i.e., it is only indirectly visible). The quantities \gamma^{\mu} are the Dirac matrices, and 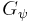G_{\psi} is the already-mentioned "Yukawa"-coupling parameter. Already now the mass-generation follows the same principle as above, namely from the existence of a finite expectation value 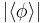|\langle\phi\rangle |, as described above. Again, this is crucial for the existence of the property "mass".

History of research

Background

Spontaneous symmetry breaking offered a framework to introduce bosons into relativistic quantum field theories. However, according to Goldstone's theorem, these bosons should be massless.[2] The only observed particles which could be approximately interpreted as Goldstone bosons were the pions, which Yoichiro Nambu related to chiral symmetry breaking.

A similar problem arises with Yang–Mills theory (also known as nonabelian gauge theory), which predicts massless spin-1 gauge bosons. Massless weakly interacting gauge bosons lead to long-range forces, which are only observed for electromagnetism and the corresponding massless photon. Gauge theories of the weak force needed a way to describe massive gauge bosons in order to be consistent.

Discovery

The Higgs mechanism is also called the Brout–Englert–Higgs mechanism, or Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism,[3] or Anderson–Higgs mechanism. The mechanism was proposed in 1962 by Philip Warren Anderson,[4] who discussed its consequences for particle physics but did not work out an explicit relativistic model. The relativistic model was developed in 1964 by Peter Higgs,[5] and independently by Robert Brout and Francois Englert,[6] and Gerald Guralnik, C. R. Hagen, and Tom Kibble,[7] who worked out the results by the spring of 1963.[8] The mechanism is closely analogous to phenomena previously discovered by Yoichiro Nambu involving the "vacuum structure" of quantum fields in superconductivity.[9] A similar but distinct effect, known as the Stueckelberg mechanism, had previously been studied by Ernst Stueckelberg. These physicists discovered that when a gauge theory is combined with an additional field breaking spontaneously the symmetry group, the gauge bosons can consistently acquire a finite mass. In spite of the large values involved (see below) this permits a gauge theory description of the weak force, which was independently developed by Steven Weinberg and Abdus Salam in 1967. Higgs's original article presenting the model was rejected by Physics Letters. When revising the article before resubmitting it to Physical Review Letters, he added a sentence at the end,[10] mentioning that it implies the existence of one or more new, massive scalar bosons, which do not form complete representations of the symmetry group; these are the Higgs bosons.

The three papers by Brout and Englert; Higgs; and Guralnik, Hagen, and Kibble were each recognized as "milestone letters" by Physical Review Letters in 2008.[11] While each of these seminal papers took similar approaches, the contributions and differences among the 1964 PRL symmetry breaking papers are noteworthy. All six physicists were jointly awarded the 2010 J. J. Sakurai Prize for Theoretical Particle Physics for this work.[12]

Benjamin W. Lee is often credited with first naming the "Higgs-like" mechanism, although there is debate around when this first occurred.[13][14][15] One of the first times the Higgs name appeared in print was in 1972 when Gerardus 't Hooft and Martinus J. G. Veltman referred to it as the "Higgs-Kibble mechanism" in their Nobel winning paper.[16][17]

Examples of Higgs mechanism

The Higgs mechanism occurs whenever a charged field has a vacuum expectation value. In the nonrelativistic context, this is the Landau model of a charged Bose-Einstein condensate, also known as a superconductor. In the relativistic condensate, the condensate is a scalar field, and is relativistically invariant.

Landau Model

The Higgs mechanism is a type of superconductivity which occurs in the vacuum. It occurs when all of space is filled with a sea of particles which are charged, or, in field language, when a charged field has a nonzero vacuum expectation value. Interaction with the quantum fluid filling the space prevents certain forces from propagating over long distances (as it does in a superconducting medium, e.g. in the Ginzburg–Landau theory).

A superconductor expels all magnetic fields from its interior, a phenomenon known as the Meissner effect. This was mysterious for a long time, because it implies that electromagnetic forces somehow become short-range inside the superconductor. Contrast this with the behavior of an ordinary metal. In a metal, the conductivity shields electric fields by rearranging charges on the surface until the total field cancels in the interior. But magnetic fields can penetrate to any distance, and if a magnetic monopole (an isolated magnetic pole) is surrounded by a metal the field can escape without collimating into a string. In a superconductor, however, electric charges move with no dissipation, and this allows for permanent surface currents, not just surface charges. When magnetic fields are introduced at the boundary of a superconductor, they produce surface currents which exactly neutralize them. The Meissner effect is due to currents in a thin surface layer, whose thickness, the London penetration depth, can be calculated from a simple model (the Ginzburg–Landau theory).

This simple model treats superconductivity as a charged Bose–Einstein condensate. Suppose that a superconductor contains bosons with charge q. The wavefunction of the bosons can be described by introducing a quantum field, ψ, which obeys the Schrödinger equation as a field equation (in units where 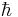\hbar, the Planck quantum divided by 2π, is replaced by 1):

i{\partial \over \partial t} \psi = {(\nabla - iqA)^2 \over 2m} \psi

The operator ψ(x) annihilates a boson at the point x, while its adjoint 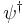\psi^\dagger creates a new boson at the same point. The wavefunction of the Bose–Einstein condensate is then the expectation value ψ of ψ(x), which is a classical function that obeys the same equation. The interpretation of the expectation value is that it is the phase that one should give to a newly created boson so that it will coherently superpose with all the other bosons already in the condensate.

When there is a charged condensate, the electromagnetic interactions are screened. To see this, consider the effect of a gauge transformation on the field. A gauge transformation rotates the phase of the condensate by an amount which changes from point to point, and shifts the vector potential by a gradient.

\psi \rightarrow e^{iq\phi(x)} \psi
A \rightarrow A %2B \nabla \phi

When there is no condensate, this transformation only changes the definition of the phase of ψ at every point. But when there is a condensate, the phase of the condensate defines a preferred choice of phase.

The condensate wave function can be written as

\psi(x) = \rho(x)\, e^{i\theta(x)},

where ρ is real amplitude, which determines the local density of the condensate. If the condensate were neutral, the flow would be along the gradients of θ, the direction in which the phase of the Schrödinger field changes. If the phase θ changes slowly, the flow is slow and has very little energy. But now θ can be made equal to zero just by making a gauge transformation to rotate the phase of the field.

The energy of slow changes of phase can be calculated from the Schrödinger kinetic energy,

H= {1\over 2m} |{(qA%2B\nabla )\psi|^2},

and taking the density of the condensate ρ to be constant,

H \approx {\rho^2 \over 2m} (qA %2B \nabla \theta)^2.

Fixing the choice of gauge so that the condensate has the same phase everywhere, the electromagnetic field energy has an extra term,

{q^2 \rho^2 \over 2m} A^2.

When this term is present, electromagnetic interactions become short-ranged. Every field mode, no matter how long the wavelength, oscillates with a nonzero frequency. The lowest frequency can be read off from the energy of a long wavelength A mode,

E\approx {{\dot A}^2\over 2} %2B {q^2 \rho^2 \over 2m} A^2.

This is a harmonic oscillator with frequency:

\sqrt{\frac{1}{m} q^2 \rho^2}.

The quantity |ψ|2 (=ρ2) is the density of the condensate of superconducting particles.

In an actual superconductor, the charged particles are electrons, which are fermions not bosons. So in order to have superconductivity, the electrons need to somehow bind into Cooper pairs. The charge of the condensate q is therefore twice the electron charge e. The pairing in a normal superconductor is due to lattice vibrations, and is in fact very weak; this means that the pairs are very loosely bound. The description of a Bose–Einstein condensate of loosely bound pairs is actually more difficult than the description of a condensate of elementary particles, and was only worked out in 1957 by Bardeen, Cooper and Schrieffer in the famous BCS theory.

Abelian Higgs Mechanism

Gauge invariance means that certain transformations of the gauge field do not change the energy at all. If an arbitrary gradient is added to A, the energy of the field is exactly the same. This makes it difficult to add a mass term, because a mass term tends to push the field toward the value zero. But the zero value of the vector potential is not a gauge invariant idea. What is zero in one gauge is nonzero in another.

So in order to give mass to a gauge theory, the gauge invariance must be broken by a condensate. The condensate will then define a preferred phase, and the phase of the condensate will define the zero value of the field in a gauge invariant way. The gauge invariant definition is that a gauge field is zero when the phase change along any path from parallel transport is equal to the phase difference in the condensate wavefunction.

The condensate value is described by a quantum field with an expectation value, just as in the Landau–Ginzburg model.

In order for the phase of the vacuum to define a gauge, the field must have a phase (also referred to as 'to be charged'). In order for a scalar field Φ to have a phase, it must be complex, or (equivalently) it should contain two fields with a symmetry which rotates them into each other. The vector potential changes the phase of the quanta produced by the field when they move from point to point. In terms of fields, it defines how much to rotate the real and imaginary parts of the fields into each other when comparing field values at nearby points.

The only renormalizable model where a complex scalar field Φ acquires a nonzero value is the Mexican-hat model, where the field energy has a minimum away from zero.

S(\phi ) = \int {1\over 2} |\partial \phi|^2 - \lambda\cdot (|\phi|^2 - \Phi^2)^2

This defines the following Hamiltonian:

H(\phi ) = {1\over 2} |\dot\phi|^2 %2B |\nabla \phi|^2 %2B V(|\phi|)

The first term is the kinetic energy of the field. The second term is the extra potential energy when the field varies from point to point. The third term is the potential energy when the field has any given magnitude.

This potential energy V(z, Φ) = λ • (|z|2 - Φ2)2 has a graph which looks like a Mexican hat, which gives the model its name. In particular, the minimum energy value is not at z = 0, but on the circle of points where the magnitude of z is Φ.

When the field Φ(x) is not coupled to electromagnetism, the Mexican-hat potential has flat directions. Starting in any one of the circle of vacua and changing the phase of the field from point to point costs very little energy. Mathematically, if

\phi(x) = \Phi e^{i\theta(x)}

with a constant prefactor, then the action for the field θ(x), i.e., the "phase" of the Higgs field Φ(x), has only derivative terms. This is not a surprise. Adding a constant to θ(x) is a symmetry of the original theory, so different values of θ(x) cannot have different energies. This is an example of Goldstone's theorem: spontaneously broken continuous symmetries normally produce massless excitations.

The Abelian Higgs model is the Mexican-hat model coupled to electromagnetism:

S(\phi ,A) = \int {1\over 4} F^{\mu\nu} F_{\mu\nu} %2B |(\partial - i q A)\phi|^2 %2B \lambda\cdot (|\phi|^2 - \Phi^2)^2.

The classical vacuum is again at the minimum of the potential, where the magnitude of the complex field φ is equal to Φ. But now the phase of the field is arbitrary, because gauge transformations change it. This means that the field θ(x) can be set to zero by a gauge transformation, and does not represent any actual degrees of freedom at all.

Furthermore, choosing a gauge where the phase of the vacuum is fixed, the potential energy for fluctuations of the vector field is nonzero. So in the abelian Higgs model, the gauge field acquires a mass. To calculate the magnitude of the mass, consider a constant value of the vector potential A in the x direction in the gauge where the condensate has constant phase. This is the same as a sinusoidally varying condensate in the gauge where the vector potential is zero. In the gauge where A is zero, the potential energy density in the condensate is the scalar gradient energy:

E = {1 \over 2} \left |\partial \left (\Phi e^{iqAx} \right ) \right |^2 = {1 \over 2} q^2\Phi^2 A^2

And this energy is the same as a mass term ½m2A2 where m = qΦ.

Nonabelian Higgs mechanism

The Nonabelian Higgs model has the following action:

S(\phi ,\mathbf A) = \int {1\over 4g^2} \mathop{\textrm{tr}}(F^{\mu\nu}F_{\mu\nu}) %2B |D\phi|^2 %2B V(|\phi|)

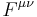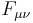where now the nonabelian field A is contained in D and in the tensor components F^{\mu \nu} and F_{\mu \nu} (the relation between A and those components is well-known from the Yang–Mills theory).

It is exactly analogous to the Abelian Higgs model. Now the field φ is in a representation of the gauge group, and the gauge covariant derivative is defined by the rate of change of the field minus the rate of change from parallel transport using the gauge field A as a connection.

D\phi = \partial \phi - i A^k t_k \phi

Again, the expectation value of Φ defines a preferred gauge where the vacuum is constant, and fixing this gauge, fluctuations in the gauge field A come with a nonzero energy cost.

Depending on the representation of the scalar field, not every gauge field acquires a mass. A simple example is in the renormalizable version of an early electroweak model due to Julian Schwinger. In this model, the gauge group is SO(3) (or SU(2)--- there are no spinor representations in the model), and the gauge invariance is broken down to U(1) or SO(2) at long distances. To make a consistent renormalizable version using the Higgs mechanism, introduce a scalar field φa which transforms as a vector (a triplet) of SO(3). If this field has a vacuum expectation value, it points in some direction in field space. Without loss of generality, one can choose the z-axis in field space to be the direction that φ is pointing, and then the vacuum expectation value of φ is (0, 0, A), where A is a constant with dimensions of mass (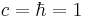c = \hbar = 1).

Rotations around the z-axis form a U(1) subgroup of SO(3) which preserves the vacuum expectation value of φ, and this is the unbroken gauge group. Rotations around the x and y-axis do not preserve the vacuum, and the components of the SO(3) gauge field which generate these rotations become massive vector mesons. There are two massive W mesons in the Schwinger model, with a mass set by the mass scale A, and one massless U(1) gauge boson, similar to the photon.

The Schwinger model predicts magnetic monopoles at the electroweak unification scale, and does not predict the Z meson. It doesn't break electroweak symmetry properly as in nature. But historically, a model similar to this (but not using the Higgs mechanism) was the first in which the weak force and the electromagnetic force were unified.

Affine Higgs mechanism

Ernst Stueckelberg discovered a version of the Higgs mechanism by analyzing the theory of quantum electrodynamics with a massive photon. Stueckelberg's model is a limit of the regular Mexican hat Abelian Higgs model, where the vacuum expectation value H goes to infinity and the charge of the Higgs field goes to zero in such a way that their product stays fixed. The mass of the Higgs boson is proportional to H, so the Higgs boson becomes infinitely massive and disappears. The vector meson mass is equal to the product eH, and stays finite.

The interpretation is that when a U(1) gauge field does not require quantized charges, it is possible to keep only the angular part of the Higgs oscillations, and discard the radial part. The angular part of the Higgs field θ has the following gauge transformation law:

\theta \rightarrow \theta %2B e\alpha\,
A \rightarrow A %2B \alpha \,

The gauge covariant derivative for the angle (which is actually gauge invariant) is:

D\theta = \partial \theta - e A\,

In order to keep θ fluctuations finite and nonzero in this limit, θ should be rescaled by H, so that its kinetic term in the action stays normalized. The action for the theta field is read off from the Mexican hat action by substituting 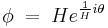\phi \;=\; He^{\frac{1}{H}i\theta}.

S = \int {1 \over 4}F^2 %2B {1 \over 2}(D\theta)^2 = \int {1 \over 4}F^2 %2B {1 \over 2}(\partial \theta - He A)^2 = \int {1 \over 4}F^2 %2B {1 \over 2}(\partial \theta - m A)^2

since eH is the gauge boson mass. By making a gauge transformation to set θ = 0, the gauge freedom in the action is eliminated, and the action becomes that of a massive vector field:

S= \int {1 \over 4} F^2 %2B {1 \over 2} m^2 A^2\,

To have arbitrarily small charges requires that the U(1) is not the circle of unit complex numbers under multiplication, but the real numbers R under addition, which is only different in the global topology. Such a U(1) group is non-compact. The field θ transforms as an affine representation of the gauge group. Among the allowed gauge groups, only non-compact U(1) admits affine representations, and the U(1) of electromagnetism is experimentally known to be compact, since charge quantization holds to extremely high accuracy.

The Higgs condensate in this model has infinitesimal charge, so interactions with the Higgs boson do not violate charge conservation. The theory of quantum electrodynamics with a massive photon is still a renormalizable theory, one in which electric charge is still conserved, but magnetic monopoles are not allowed. For nonabelian gauge theory, there is no affine limit, and the Higgs oscillations cannot be too much more massive than the vectors.

See also

References

  1. ^ G. Bernardi, M. Carena, and T. Junk: "Higgs bosons: theory and searches", Reviews of Particle Data Group: Hypothetical particles and Concepts, 2007, http://pdg.lbl.gov/2008/reviews/higgs_s055.pdf
  2. ^ Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2
  3. ^ Englert-Brout-Higgs-Guralnik-Hagen-Kibble Mechanism on Scholarpedia
  4. ^ P. W. Anderson (1962). "Plasmons, Gauge Invariance, and Mass". Physical Review 130 (1): 439–442. Bibcode 1963PhRv..130..439A. doi:10.1103/PhysRev.130.439. 
  5. ^ Peter W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters 13 (16): 508–509. Bibcode 1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508. 
  6. ^ F. Englert and R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters 13 (9): 321–323. Bibcode 1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321. 
  7. ^ G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters 13 (20): 585–587. Bibcode 1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585. 
  8. ^ Gerald S. Guralnik (2009). "The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles". International Journal of Modern Physics A24 (14): 2601–2627. arXiv:0907.3466. Bibcode 2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431. 
  9. ^ Nambu, Y (1960). "Quasiparticles and Gauge Invariance in the Theory of Superconductivity". Physical Review 117 (3): 648–663. Bibcode 1960PhRv..117..648N. doi:10.1103/PhysRev.117.648. 
  10. ^ Higgs, Peter (2007). "Prehistory of the Higgs boson". Comptes Rendus Physique 8 (9): 970–972. Bibcode 2007CRPhy...8..970H. doi:10.1016/j.crhy.2006.12.006 
  11. ^ Physical Review Letters – 50th Anniversary Milestone Papers
  12. ^ American Physical Society – J. J. Sakurai Prize Winners
  13. ^ Rochester's Hagen Sakurai Prize Announcement
  14. ^ C.R. Hagen discusses naming of Higgs Boson in 2010 Sakurai Prize Talk
  15. ^ Anything but the God particle by Ian Sample
  16. ^ G. 't Hooft and M. Veltman (1972). "Regularization and Renormalization of Gauge Fields". Nuclear Physics B 44 (1): 189–219. Bibcode 1972NuPhB..44..189T. doi:10.1016/0550-3213(72)90279-9. 
  17. ^ Regularization and Renormalization of Gauge Fields by t'Hooft and Veltman (PDF)

Further reading

External links