Hessian affine region detector

Feature detection
Output of a typical corner detection algorithm
Edge detection
Canny · Canny-Deriche · Differential · Sobel · Prewitt · Roberts Cross
Interest point detection
Corner detection
Harris operator · Shi and Tomasi · Level curve curvature · SUSAN · FAST
Blob detection
Laplacian of Gaussian (LoG) · Difference of Gaussians (DoG) · Determinant of Hessian (DoH) · Maximally stable extremal regions · PCBR
Ridge detection
Hough transform
Structure tensor
Affine invariant feature detection
Affine shape adaptation · Harris affine · Hessian affine
Feature description
SIFT · SURF · GLOH · HOG · LESH
Scale-space
Scale-space axioms · Implementation details · Pyramids

The Hessian affine region detector is a feature detector used in the fields of computer vision and image analysis. Like other feature detectors, the Hessian affine detector is typically used as a preprocessing step to algorithms that rely on identifiable, characteristic interest points.

The Hessian affine detector is part of the subclass of feature detectors known as affine-invariant detectors: Harris affine region detector, Hessian affine regions, maximally stable extremal regions, Kadir–Brady saliency detector, edge-based regions (EBR) and intensity-extrema-based (IBR) regions.

Contents

Algorithm description

The Hessian affine detector algorithm is almost identical to the Harris affine region detector. In fact, both algorithms were derived by Krystian Mikolajczyk and Cordelia Schmid in 2002, ,[1] based on earlier work in,[2][3] see also [4] for a more general overview. See the Harris affine region detector entry for a more complete description of the detection algorithm.

How does the Hessian affine differ?

The Harris affine detector relies on interest points detected at multiple scales using the Harris corner measure on the second-moment matrix. The Hessian affine also uses a multiple scale iterative algorithm to spatially localize and select scale & affine invariant points. However, at each individual scale, the Hessian affine detector chooses interest points based on the Hessian matrix at that point:

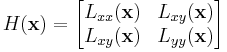
H(\mathbf{x}) = \begin{bmatrix} L_{xx}(\mathbf{x}) & L_{xy}(\mathbf{x})\\ L_{xy}(\mathbf{x}) & L_{yy}(\mathbf{x})\\ \end{bmatrix}

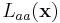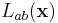where L_{aa}(\mathbf{x}) is second partial derivative in the a direction and L_{ab}(\mathbf{x}) is the mixed partial second derivative in the a and b directions. It's important to note that the derivatives are computed in the current iteration scale and thus are derivatives of an image smoothed by a Gaussian kernel: L(\mathbf{x}) = g(\sigma_I) \otimes I(\mathbf{x}) . 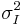As discussed in the Harris affine region detector article, the derivatives must be scaled appropriately by a factor related to the Gaussian kernel: \sigma_I^2.

At each scale, interest points are those points that simultaneously are local extrema of both the determinant and trace of the Hessian matrix. The trace of Hessian matrix is identical to the Laplacian of Gaussians (LoG)[5]:

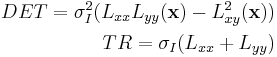
\begin{align} DET = \sigma_I^2 ( L_{xx}L_{yy}(\mathbf{x}) - L_{xy}^2(\mathbf{x})) \\ TR = \sigma_I (L_{xx} %2B L_{yy}) \end{align}

As discussed in Mikolajczyk et al.(2005), by choosing points that maximize the determinant of the Hessian, this measure penalizes longer structures that have small second derivatives (signal changes) in a single direction.[6] This type of measure is very similar to the measures used in the blob detection schemes proposed by Lindeberg (1998), where either the Laplacian or the determinant of the Hessian were used in blob detection methods with automatic scale selection.

Like the Harris affine algorithm, these interest points based on the Hessian matrix are also spatially localized using an iterative search based on the Laplacian of Gaussians. Predictably, these interest points are called Hessian–Laplace interest points. Furthermore, using these initially detected points, the Hessian affine detector uses an iterative shape adaptation algorithm to compute the local affine transformation for each interest point. The implementation of this algorithm is almost identical to that of the Harris affine detector; however, the above mentioned Hessian measure replaces all instances of the Harris corner measure.

Robustness to affine and other transformations

Mikolajczyk et al. (2005) have done a thorough analysis of several state of the art affine region detectors: Harris affine, Hessian affine, MSER,[7] IBR & EBR [8] and salient[9] detectors.[6] Mikolajczyk et al. analyzed both structured images and textured images in their evaluation. Linux binaries of the detectors and their test images are freely available at their webpage. A brief summary of the results of Mikolajczyk et al. (2005) follow; see A comparison of affine region detectors for a more quantitative analysis.

Overall, the Hessian affine detector performs second best to MSER. Like the Harris affine detector, Hessian affine interest regions tend to be more numerous and smaller than other detectors. For a single image, the Hessian affine detector typically identifies more reliable regions than the Harris-Affine detector. The performance changes depending on the type of scene being analyzed. The Hessian affine detector responds well to textured scenes in which there are a lot of corner-like parts. However, for some structured scenes, like buildings, the Hessian affine detector performs very well. This is complementary to MSER that tends to do better with well structured (segmentable) scenes.

Software packages

External links

See also

References

  1. ^ Mikolajcyk, K. and Schmid, C. 2002. An affine invariant interest point detector. In Proceedings of the 8th International Conference on Computer Vision, Vancouver, Canada.
  2. ^ Lindeberg, Tony. "Feature detection with automatic scale selection", International Journal of Computer Vision, 30, 2, pp. 77-116, 1998.
  3. ^ T. Lindeberg and J. Garding (1997). "Shape-adapted smoothing in estimation of 3-D depth cues from affine distortions of local 2-D structure". Image and Vision Computing 15 (6): pp 415–434. doi:10.1016/S0262-8856(97)01144-X. http://www.nada.kth.se/~tony/abstracts/LG94-ECCV.html. 
  4. ^ T. Lindeberg (2008/2009). "Scale-space". Encyclopedia of Computer Science and Engineering (Benjamin Wah, ed), John Wiley and Sons IV: 2495–2504. doi:10.1002/9780470050118.ecse609. http://www.nada.kth.se/~tony/abstracts/Lin08-EncCompSci.html. 
  5. ^ Mikolajczykm K. and Schmid, C. 2004. Scale & affine invariant interest point detectors. International Journal on Computer Vision 60(1):63-86.
  6. ^ a b K. Mikolajczyk, T. Tuytelaars, C. Schmid, A. Zisserman, J. Matas, F. Schaffalitzky, T. Kadir and L. Van Gool, A comparison of affine region detectors. In IJCV 65(1/2):43-72, 2005
  7. ^ J.Matas, O. Chum, M. Urban, and T. Pajdla, Robust wide baseline stereo from maximally stable extremal regions. In BMVC p. 384-393, 2002.
  8. ^ T.Tuytelaars and L. Van Gool, Matching widely separated views based on affine invariant regions . In IJCV 59(1):61-85, 2004.
  9. ^ T. Kadir, A. Zisserman, and M. Brady, An affine invariant salient region detector. In ECCV p. 404-416, 2004.