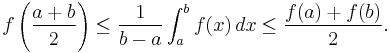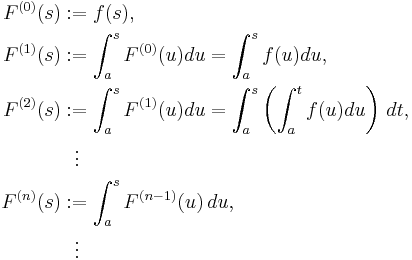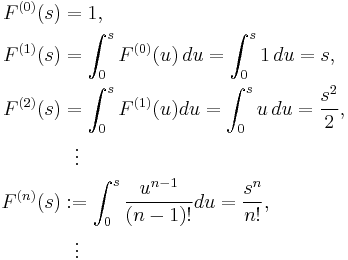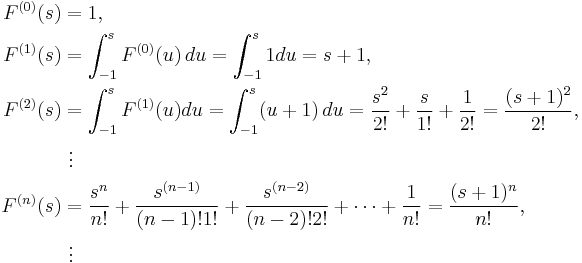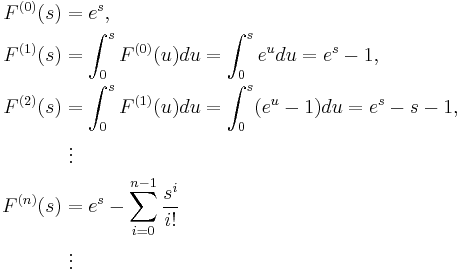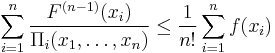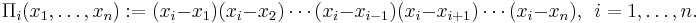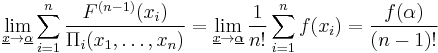Hermite–Hadamard inequality
In mathematics, the Hermite–Hadamard inequality, named after Charles Hermite and Jacques Hadamard and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex, then
One of the most natural extension of the right side of this classical enequality is due to Zoltán Retkes. For to formulate this result one has to introduce the notion of iterated integrals.
Contents |
The concept of the sequence of iterated integrals
Suppose that −∞ < a < b < ∞, and let f:[a, b] → ℝ be an integrable real function. Under the above conditions the following sequence of functions is called the sequence of iterated integrals of f,where a ≤ s ≤ b.:
Example 1
Let [a, b] = [0, 1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [0, 1], and
Example 2
Let [a,b] = [−1,1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [−1, 1], and
Example 3
Let [a, b] = [0, 1] and f(s) = es. Then the sequence of iterated integrals of f is defined on [0, 1], and
Theorem (Retkes inequality)
Suppose that −∞ < a < b < ∞, and let f:[a,b]→R be a convex function, a < xi < b, i = 1, ..., n, such that xi ≠ xj, if i ≠ j. Then the following holds:
where
In the concave case ≤ is changed to ≥.
Remark 1. If f is convex in the strict sense then ≤ is changed to < and equality holds iff f is linear function.
Remark 2. The inequality is sharp in the following limit sense: let 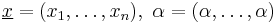 and
and 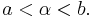
Then the limit of the left side exists and
References
- Jacques Hadamard, "Étude sur les propriétés des fonctions entières et en particulier d'une fonction considérée par Riemann", Journal de Mathématiques Pures et Appliquées, volume 58, 1893, pages 171–215.
- Zoltán Retkes, "An extension of the Hermite–Hadamard Inequality", Acta Sci. Math. (Szeged), 74 (2008), pages 95–106.
- Mihály Bessenyei, "The Hermite–Hadamard Inequality on Simplices", American Mathematical Monthly, volume 115, April 2008, pages 339–345.