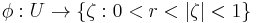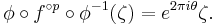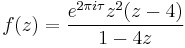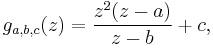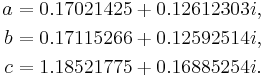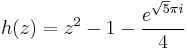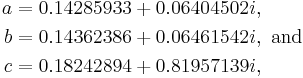Herman ring

In the mathematical discipline known as complex dynamics for rational functions, the Herman ring is a Fatou component.[1] where the rational function is conformally conjugate to a irrational rotation of the standard annulus.

Contents

Formal definition

Namely if ƒ possesses a Herman ring U with period p, then there exists a conformal mapping

\phi:U\rightarrow\{\zeta:0<r<|\zeta|<1\}

and an irrational number \theta, such that

\phi\circ f^{\circ p}\circ\phi^{-1}(\zeta)=e^{2\pi i\theta}\zeta.

So the dynamics on the Herman ring is simple.

Name

It was introduced by, and later named after, Michael Herman (1979) who first found and constructed this type of Fatou component.

Examples

Here is an example of a rational function which possesses a Herman ring.[1]

f(z) = \frac{e^{2 \pi i \tau} z^2(z - 4)}{1 - 4z}

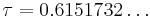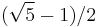where \tau=0.6151732\dots such that the rotation number of ƒ on the unit circle is (\sqrt{5}-1)/2.

The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.

There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components (see Classification of Fatou components) at the same time.

Further, there is a rational function which possesses a Herman ring with period 2.

Here the expression of this rational function is

g_{a,b,c}(z) = \frac{z^2(z-a)}{z-b} %2B c, \,

where

\begin{align} a & = 0.17021425%2B0.12612303i, \\ b & = 0.17115266%2B0.12592514i, \\ c & = 1.18521775%2B0.16885254i. \end{align}

This example was constructed by quasiconformal surgery[2] from the quadratic polynomial

h(z)=z^2 - 1 - \frac{e^{\sqrt{5}\pi i}}{4}

which possesses a Siegel disk with period 2. The parameters a, b, c are calculated by trial and error.

Letting

\begin{align} a & = 0.14285933%2B0.06404502i, \\ b & = 0.14362386%2B0.06461542i,\text{ and} \\ c & = 0.18242894%2B0.81957139i, \end{align}

then the period of one of the Herman ring of ga,b,c is 3.

Shishikura also given an example:[3] a rational function which possesses a Herman ring with period 2, but the parameters showed above are different from his.

So there is a question: How to find the formulas of the rational functions which possess Herman rings with higher period?

According to the result of Shishikura, if a rational function ƒ possesses a Herman ring, then the degree of ƒ is at least 3. There also exist meromorphic functions that possess Herman rings.

References

  1. ^ a b John Milnor, Dynamics in one complex variable: Third Edition, Annals of Mathematics Studies, 160, Princeton Univ. Press, Princeton, NJ, 2006.
  2. ^ Mitsuhiro Shishikura, On the quasiconformal surgery of rational functions. Ann. Sci. Ecole Norm. Sup. (4) 20 (1987), no. 1, 1–29.
  3. ^ Mitsuhiro Shishikura, Surgery of complex analytic dynamical systems, in "Dynamical Systems and Nonlinear Oscillations", Ed. by Giko Ikegami, World Scientic Advanced Series in Dynamical Systems, 1, World Scientic, 1986, 93–105.