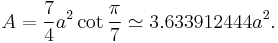Heptagon
| Regular heptagon | |
|---|---|
A regular heptagon |
|
| Edges and vertices | 7 |
| Schläfli symbol | {7} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D7) |
| Internal angle (degrees) | 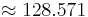 ° ° |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a heptagon is a polygon with seven sides and seven angles. In a regular heptagon, in which all sides and all angles are equal, the sides meet at an angle of 5π/7 radians, 128.5714286 degrees. Its Schläfli symbol is {7}. The area (A) of a regular heptagon of side length a is given by
The heptagon is also occasionally referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix) together with the Greek suffix "-agon" meaning angle).
Contents |
Construction
A regular heptagon is not constructible with compass and straightedge but is constructible with a marked ruler and compass. This type of construction is called a Neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that 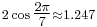 is a zero of the irreducible cubic x3 + x2 − 2x − 1. Consequently this polynomial is the minimal polynomial of 2cos(2π⁄7), whereas the degree of the minimal polynomial for a constructible number must be a power of 2.
is a zero of the irreducible cubic x3 + x2 − 2x − 1. Consequently this polynomial is the minimal polynomial of 2cos(2π⁄7), whereas the degree of the minimal polynomial for a constructible number must be a power of 2.
A Neusis construction of the interior angle in a regular heptagon. |
A Neusis construction of the interior angle in a regular heptagon. (method by John Horton Conway |
An animation of an approximate compass-and-straightedge construction of a regular heptagon. |
|
Approximation
A decent approximation for practical use with an accuracy of ≈0.2% is shown in the drawing. Let A lie on the circumference of the circumcircle. Draw arc BOC. Then 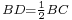 gives an approximation for the edge of the heptagon.
gives an approximation for the edge of the heptagon.
A more exact approximation
A regular heptagon with sides 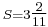 can be inscribed in a circle of radius
can be inscribed in a circle of radius 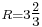 with an error of less than 0.00013%.
with an error of less than 0.00013%.
This follows from a rational approximation of 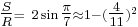 .
.
Star heptagons
Two kinds of star heptagons can be constructed from regular heptagons, labeled by Schläfli symbols {7/2}, and {7/3}, with the divisor being the interval of connection.
Blue, {7/2} and green {7/3} star heptagons inside a red heptagon.
Uses
The United Kingdom currently (2011) has two heptagonal coins, the 50p and 20p pieces, and the Barbados Dollar is also heptagonal. The 20-eurocent coin has cavities placed similarly. Strictly, the shape of the coins is a Reuleaux heptagon, a curvilinear heptagon to make them curves of constant width: the sides are curved outwards so that the coin will roll smoothly in vending machines. Botswana pula coins in the denominations of 2 Pula, 1 Pula, 50 Thebe and 5 Thebe are also shaped as equilateral-curve heptagons. Coins in the shape of Reuleaux heptagons are in circulation in Mauritius, U.A.E., Tanzania, Samoa, Papua New Guinea, São Tomé and Príncipe, Haiti, Jamaica, Liberia, Haiti, Ghana, the Gambia, Jordan, Jersey, Guernsey, Isle of Man, Gibraltar, Guyana, Solomon Islands, Falkland Islands and Saint Helena. The 1000 Kwacha coin of Zambia is a true heptagon.
The Brazilian 25-cent coin has a heptagon inscribed in the coin's disk. Some old versions of Coat of arms of Georgia including Soviet days had used {7/2} heptagram as an element.
Apart from the heptagonal prism and heptagonal antiprism, no polyhedron made entirely out of regular polygons contains a heptagon as a face.
Regular heptagons can tile the hyperbolic plane, as shown in this Poincaré disk model projection:
Graphs
The K7 complete graph is often drawn as a regular heptagon with all 21 edges connected. This graph also represents an orthographic projection of the 7 vertices and 21 edges of the 6-simplex. The 21 and 35 vertices of the rectified and birectified 6-simplex also orthogonally project into regular heptagons.
6-simplex (6D) |
Rectified 6-simplex (6D) |
Birectified 6-simplex (6D) |
See also
External links
- Definition and properties of a heptagon With interactive animation
- Weisstein, Eric W., "Heptagon" from MathWorld.
- Another approximate construction method
- Polygons – Heptagons
- Recently discovered and highly accurate approximation for the construction of a regular heptagon.
|
|||||||||||||||||