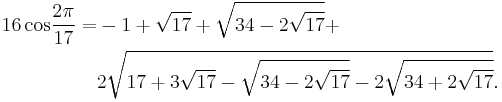Heptadecagon
| Regular heptadecagon | |
|---|---|
A regular heptadecagon |
|
| Edges and vertices | 17 |
| Schläfli symbol | {17} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D17) |
| Internal angle (degrees) |  ° |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a heptadecagon (or 17-gon) is a seventeen-sided polygon.
Contents |
Heptadecagon construction
The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19.
Constructibility implies that trigonometric functions of 2π⁄17 can be expressed with basic arithmetic and square roots alone. Gauss' book Disquisitiones Arithmeticae contains the following equation, given here in modern notation:
The first actual method of construction was devised by Johannes Erchinger, a few years after Gauss' work.
Thanks to the construction above it is easy to obtain multiples of 17 by 3 and 5 and any power of 2, for example a 34-gon, 51-gon, 85-gon or 255-gon.
Carl Friedrich Gauss proved – as a 19-year-old student at Göttingen University – that the regular heptadecagon (a 17-sided polygon) is constructible with a pair of compasses and a straightedge. His proof relies on the property of irreducible polynomial equations that roots composed of a finite number of square root extractions only exist when the order of the equation is a product of the forms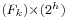 
. There are distinct primes of the form: 
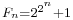, known as Fermat primes. Constructions for the regular triangle, square, pentagon, hexagon et al. had been given by Euclid, but constructions based on the Fermat primes other than 3 and 5 were unknown to the ancients. (The only known Fermat primes are Fn for n = 0, 1, 2, 3, 4. They are 3, 5, 17, 257, 65537.) The first explicit construction of a heptadecagon was given by Erchinger (see above).
Another method of construction uses Carlyle circles, as shown below:
Petrie polygons
The regular heptadecagon is the Petrie polygon for one higher-dimensional polytope, projected in a skew orthogonal projection:
16-simplex (16D) |
See also
Further reading
- Dunham, William (September 1996). "1996—a triple anniversary". Math Horizons: 8–13. http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=3057. Retrieved 2009-12-06.
- Klein, Felix et al. Famous Problems and Other Monographs. – Describes the algebraic aspect, by Gauss.
External links
- Weisstein, Eric W., "Heptadecagon" from MathWorld. Contains a description of the construction.
- "Constructing the Heptadecagon" at MathPages.com.
- Heptadecagon trigonometric functions
- heptadecagon building New R&D center for SolarUK
- BBC video of New R&D center for SolarUK
|
|||||||||||||||||