Hemorheology

Hemorheology is the study of flow properties of blood and its elements (plasma and formed elements, including red blood cells, white blood cells and platelets). There is increasing evidence indicating that flow properties of blood are among the main determinants of proper tissue perfusion and alterations in these properties play significant roles in disease processes; hence, knowledge of them is vital to any understanding of hemorheology.[1]

Introduction

In analyzing blood flows, one is generally interested in how the blood responds to forces (e.g., pressure gradients, shear stresses). The general fluid mechanical procedure used to predict how a fluid flows in response to forces involves three steps:[1]

(1) Consideration of all the forces being exerted on an infinitesimally small volume of fluid. This is done by use of the physical principle known as the conservation of momentum, and results in equations which relate the forces to velocity gradients.

(2) Introduction of rheological (“constitutive”) equations which are specific to the fluid being analyzed. These equations indicate how the fluid responds to forces, and relate the forces to the resulting velocity gradients. The rheological equations contain fluid specific characteristics (e.g., apparent viscosity as a function of shear rate).

(3) Substitution of the rheological equations into the conservation of momentum equations, and integration of the resultant differential equations to obtain macroscopic relationships, such as between flow rates and pressure gradients.

Constitutive Equations [1]

The relationships between shear stress and shear rate for blood must be determined experimentally and expressed as mathematical equations, usually referred to as constitutive equations. Given the complex macro-rheological behavior of blood, it is not surprising that a single equation fails to completely describe the effects of various rheological variables (e.g., hematocrit, shear rate). Thus, several approaches to defining these equations exist, with some the result of curve-fitting experimental data and others based on a particular rheological model. Two types of constitutive equations are given below: One type results from using empirical relationships and includes Newtonian fluids, the Bingham fluid model and the power-law fluid model. All of these use the ratio of shear stress to shear rate to define an “apparent viscosity” for blood that, with the exception of Newtonian fluids, is a function of shear rate. The other type results from the use of models of suspensions and includes an Einstein-model approach based on the volume fraction of the suspension occupied by particles (e.g., hematocrit), the Casson Equation, and an equation developed by Quemada.

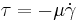
      \tau = {{-}{\mu}{\dot{\gamma}}}   
                           

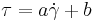
      \tau = {{a}{\dot{\gamma}} %2B{b}} 

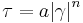
      \tau = {{a}{|\gamma|}^{n}} 

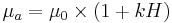
      \mu_a = {{\mu_0} \times {(1%2BkH)}} 

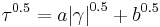
      {\tau}^{0.5} = {{a}{|\gamma|}^{0.5} %2B b^ {0.5}}  

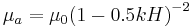
      \mu_a = {{\mu_0} {{(1-0.5kH)}^{-2}}} 

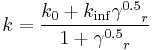
      k = {{k_0 %2B k_\inf {\gamma^{0.5}}_r  } \over {1%2B{\gamma^{0.5}}_r}} 

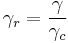
      \gamma_r = {{\gamma} \over {\gamma_c}}

Blood is a suspension of cellular elements in plasma, therefore exhibit non-Newtonian flow behavior. That is, its viscosity is shear rate dependent. Blood viscosity decrease with increased shear rate, known as shear thinning.

Blood viscosity is determined by plasma viscosity, hematocrit (volume fraction of red blood cell, which constitute 99.9% of the cellular elements) and mechanical behavior of red blood cells. Therefore, red blood cell mechanics is the major determinant of flow properties of blood. Red blood cells have unique mechanical behavior, which can be discussed under the terms “erythrocyte deformability” and “erythrocyte aggregation”.[2]

Blood viscosity can be measured by viscometers capable of measurements at various shear rates, such as a rotational viscometer.[3]

The Fåhraeus Effect

The finding that, for blood flowing steadily in tubes with diameters of less than 300 micrometres, the average hematocrit of the blood in the tube is less than the hematocrit of the blood in the reservoir feeding the tube is known as the Fåhraeus Effect. This effect is generated in the concentration entrance length of the tube, in which erythrocytes move towards the central region of the tube as they flow downstream. This entrance length is estimated to be about the distance that the blood travels in a quarter of a second for blood where red blood cell aggregation is negligible and the vessel diameter is greater than about 20 micrometres.[1]

The Fåhræus–Lindqvist effect

As the characteristic dimension of a flow channel approaches the size of the particles in a suspension; one should expect that the simple continuum model of the suspension will fail to be applicable. Often, this limit of the applicability of the continuum model begins to manifest itself at characteristic channel dimensions that are about 30 times the particle diameter: in the case of blood with a characteristic RBC dimension of 8 μm, an apparent failure occurs at about 300 micrometres. This was demonstrated by Fåhraeus and Lindqvist, who found that the apparent viscosity of blood was a function of tube diameter, for diameters of 300 micrometres and less, when they flowed constant-hematocrit blood from a well-stirred reservoir through a tube. The finding that for small tubes with diameters below about 300 micrometres and for faster flow rates which do not allow appreciable erythrocyte aggregation, the effective viscosity of the blood depends on tube diameter is known as the Fåhraeus-Lindqvist Effect.[1]

Special Problems in Measuring Blood Rheology[1]

There are three properties of blood, and related fluids, which can lead to difficulties in measuring rheological properties:

  1. The plasma proteins are surfactants and form a protein layer or film at fluid-air interfaces;
  2. The erythrocytes are denser than plasma;
  3. At low shear rates, the erythrocytes aggregate.

Procedures to minimize or eliminate the influence of the protein layer depend on the type of viscometer used for the measurements. Red cell sedimentation is slow for individual cells, since the density difference between the cell(and the plasma is small. If the suspending medium is serum and thus does not promote RBC aggregation, and if the RBC volume fraction H (i.e., hematocrit) is 15% or greater, the presence of neighboring red cells causes the settling to be hindered and hence slower. RBC aggregation, as seen in plasma at stasis or slow flow, greatly increases the sedimentation rate since the settling rate of particles is dependent on the square of the particle size. Erythrocyte aggregation also causes another effect termed red cell syneresis. This phenomenon is the inward movement of RBC as they aggregate, leaving layers of cell-poor plasma at the walls of viscometers of all types.

References

  1. ^ a b c d e f Baskurt, OK; Hardeman M, Rampling MW, Meiselman HJ (2007). Handbook of Hemorheology and Hemodynamics. Amsterdam, Netherlands: IOS Press. ISBN 978-1-58603-771-1. 
  2. ^ Baskurt OK, Meiselman HJ (2003). "Blood rheology and hemodynamics". Seminars in Thrombosis and Haemostasis 29: 435–450. doi:10.1055/s-2003-44551. PMID 14631543. 
  3. ^ Baskurt OK, Boynard M, Cokelet GC, et al (2009). "New Guidelines for Hemorheological Laboratory Techniques". Clinical Hemorheology and Microcirculation 42: 75–97.