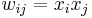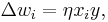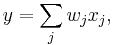Hebbian theory
Hebbian theory describes a basic mechanism for synaptic plasticity wherein an increase in synaptic efficacy arises from the presynaptic cell's repeated and persistent stimulation of the postsynaptic cell. Introduced by Donald Hebb in 1949, it is also called Hebb's rule, Hebb's postulate, and cell assembly theory, and states:
- Let us assume that the persistence or repetition of a reverberatory activity (or "trace") tends to induce lasting cellular changes that add to its stability.… When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased.
The theory is often summarized as "Cells that fire together, wire together."[1] It attempts to explain "associative learning", in which simultaneous activation of cells leads to pronounced increases in synaptic strength between those cells. Such learning is known as Hebbian learning.
Contents |
Hebbian engrams and cell assembly theory
Hebbian theory concerns how neurons might connect themselves to become engrams. Hebb's theories on the form and function of cell assemblies can be understood from the following:
- "The general idea is an old one, that any two cells or systems of cells that are repeatedly active at the same time will tend to become 'associated', so that activity in one facilitates activity in the other." (Hebb 1949, p. 70)
- "When one cell repeatedly assists in firing another, the axon of the first cell develops synaptic knobs (or enlarges them if they already exist) in contact with the soma of the second cell." (Hebb 1949, p. 63)
Gordon Allport posits additional ideas regarding cell assembly theory and its role in forming engrams, along the lines of the concept of auto-association, described as follows:
- "If the inputs to a system cause the same pattern of activity to occur repeatedly, the set of active elements constituting that pattern will become increasingly strongly interassociated. That is, each element will tend to turn on every other element and (with negative weights) to turn off the elements that do not form part of the pattern. To put it another way, the pattern as a whole will become 'auto-associated'. We may call a learned (auto-associated) pattern an engram." (Allport 1985, p. 44)
Hebbian theory has been the primary basis for the conventional view that when analyzed from a holistic level, engrams are neuronal nets or neural networks.
Work in the laboratory of Eric Kandel has provided evidence for the involvement of Hebbian learning mechanisms at synapses in the marine gastropod Aplysia californica.
Experiments on Hebbian synapse modification mechanisms at the central nervous system synapses of vertebrates are much more difficult to control than are experiments with the relatively simple peripheral nervous system synapses studied in marine invertebrates. Much of the work on long-lasting synaptic changes between vertebrate neurons (such as long-term potentiation) involves the use of non-physiological experimental stimulation of brain cells. However, some of the physiologically relevant synapse modification mechanisms that have been studied in vertebrate brains do seem to be examples of Hebbian processes. One such study reviews results from experiments that indicate that long-lasting changes in synaptic strengths can be induced by physiologically relevant synaptic activity working through both Hebbian and non-Hebbian mechanisms
Principles
From the point of view of artificial neurons and artificial neural networks, Hebb's principle can be described as a method of determining how to alter the weights between model neurons. The weight between two neurons increases if the two neurons activate simultaneously—and reduces if they activate separately. Nodes that tend to be either both positive or both negative at the same time have strong positive weights, while those that tend to be opposite have strong negative weights.
This original principle is perhaps the simplest form of weight selection. While this means it can be relatively easily coded into a computer program and used to update the weights for a network, it also prohibits the number of applications of Hebbian learning. Today, the term Hebbian learning generally refers to some form of mathematical abstraction of the original principle proposed by Hebb. In this sense, Hebbian learning involves weights between learning nodes being adjusted so that each weight better represents the relationship between the nodes. As such, many learning methods can be considered to be somewhat Hebbian in nature.
The following is a formulaic description of Hebbian learning: (note that many other descriptions are possible)
where 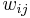 is the weight of the connection from neuron
is the weight of the connection from neuron  to neuron
to neuron  and
and  the input for neuron
the input for neuron  . Note that this is pattern learning (weights updated after every training example). In a Hopfield network, connections
. Note that this is pattern learning (weights updated after every training example). In a Hopfield network, connections 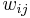 are set to zero if
are set to zero if 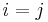 (no reflexive connections allowed). With binary neurons (activations either 0 or 1), connections would be set to 1 if the connected neurons have the same activation for a pattern.
(no reflexive connections allowed). With binary neurons (activations either 0 or 1), connections would be set to 1 if the connected neurons have the same activation for a pattern.
Another formulaic description is:
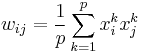 ,
,
where 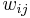 is the weight of the connection from neuron
is the weight of the connection from neuron  to neuron
to neuron  ,
,  is the number of training patterns, and
is the number of training patterns, and 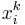 the
the  th input for neuron
th input for neuron  . This is learning by epoch (weights updated after all the training examples are presented). Again, in a Hopfield network, connections
. This is learning by epoch (weights updated after all the training examples are presented). Again, in a Hopfield network, connections 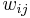 are set to zero if
are set to zero if 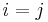 (no reflexive connections).
(no reflexive connections).
A variation of Hebbian learning that takes into account phenomena such as blocking and many other neural learning phenomena is the mathematical model of Harry Klopf. Klopf's model reproduces a great many biological phenomena, and is also simple to implement.
Generalization and stability
Hebb's Rule is often generalized as
or the change in the  th synaptic weight
th synaptic weight 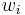 is equal to a learning rate
is equal to a learning rate 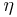 times the
times the  th input
th input  times the postsynaptic response
times the postsynaptic response  . Often cited is the case of a linear neuron,
. Often cited is the case of a linear neuron,
and the previous section's simplification takes both the learning rate and the input weights to be 1. This version of the rule is clearly unstable, as in any network with a dominant signal the synaptic weights will increase or decrease exponentially. However, it can be shown that for any neuron model, Hebb's rule is unstable. Therefore, network models of neurons usually employ other learning theories such as BCM theory, Oja's rule,[2] or the Generalized Hebbian Algorithm.
See also
- Dale's principle
- Coincidence Detection in Neurobiology
- Leabra
- Long-term potentiation
- Memory
- Metaplasticity
- Spike-timing-dependent plasticity
- Tetanic stimulation
References
- ^ See for example Doidge, Norman (2007). The Brain That Changes Itself. United States: Viking Press. pp. 427. ISBN 067003830X. http://www.normandoidge.com/normandoidge/MAIN.html.
- ^ Shouval, Harel (2005-01-03). "The Physics of the Brain". The Synaptic basis for Learning and Memory: A theoretical approach. The University of Texas Health Science Center at Houston. Archived from the original on 2007-06-10. http://web.archive.org/web/20070610134104/http://nba.uth.tmc.edu/homepage/shouval/Hebb_PCA.ppt. Retrieved 2007-11-14.
Further reading
- Hebb, D.O. (1949). The organization of behavior. New York: Wiley & Sons
- Hebb, D.O. (1961). "Distinctive features of learning in the higher animal". In J. F. Delafresnaye (Ed.). Brain Mechanisms and Learning. London: Oxford University Press.
- Hebb, D.O.; and Penfield, W. (1940). "Human behaviour after extensive bilateral removal from the frontal lobes". Archives of Neurology and Psychiatry 44: 421–436.
- Allport, D.A. (1985). "Distributed memory, modular systems and dysphasia". In Newman, S.K. and Epstein, R. (Eds.). Current Perspectives in Dysphasia. Edinburgh: Churchill Livingstone. ISBN 0-443-03039-1.
- Bishop, C.M. (1995). Neural Networks for Pattern Recognition. Oxford: Oxford University Press. ISBN 0-19-853849-9 (hardback).
- Paulsen, O.; Sejnowski, T. J. (2000). "Natural patterns of activity and long-term synaptic plasticity". Current opinion in neurobiology 10 (2): 172–179. doi:10.1016/S0959-4388(00)00076-3. PMC 2900254. PMID 10753798. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2900254.
External links
- Overview
- Hebbian Learning tutorial (Part 1: Novelty Filtering, Part 2: PCA)
|
||||||||||||||