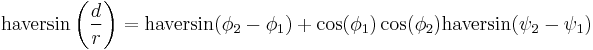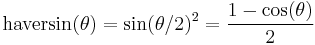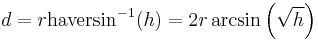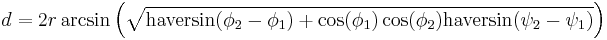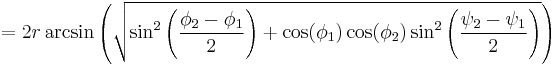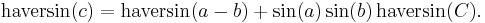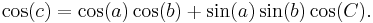Haversine formula
The haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes. It is a special case of a more general formula in spherical trigonometry, the law of haversines, relating the sides and angles of spherical "triangles".
These names follow from the fact that they are customarily written in terms of the haversine function, given by haversin(θ) = sin2(θ/2). The formulas could equally be written in terms of any multiple of the haversine, such as the older versine function (twice the haversine). Historically, the haversine had, perhaps, a slight advantage in that its maximum is one, so that logarithmic tables of its values could end at zero. These days, the haversine form is also convenient in that it has no coefficient in front of the sin2 function.
Contents |
The haversine formula
For any two points on a sphere:
where
- haversin is the haversine function:
- d is the distance between the two points (along a great circle of the sphere; see spherical distance),
- r is the radius of the sphere,
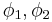 : latitude of point 1 and latitude of point 2
: latitude of point 1 and latitude of point 2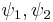 : longitude of point 1 and longitude of point 2
: longitude of point 1 and longitude of point 2
On the left side of the equals sign, the argument to the haversine function is in radians. In degrees, haversin(d/R) in the formula would become haversin(180° d/πR).
One can then solve for d either by simply applying the inverse haversine (if available) or by using the arcsine (inverse sine) function:
where
- h is haversin(d/R)
In the era before the digital calculator, the use of detailed printed tables for the haversine/inverse-haversine and its logarithm (to aid multiplications) saved navigators from squaring sines, computing square roots, etc., a process both arduous and likely to exacerbate small errors (see also versine).
When using these formulae, care must be taken to ensure that h does not exceed 1 due to a floating point error (d is only real for h from 0 to 1). h only approaches 1 for antipodal points (on opposite sides of the sphere) — in this region, relatively large numerical errors tend to arise in the formula when finite precision is used. However, because d is then large (approaching πR, half the circumference) a small error is often not a major concern in this unusual case (although there are other great-circle distance formulas that avoid this problem). (The formula above is sometimes written in terms of the arctangent function, but this suffers from similar numerical problems near h = 1.)
As described below, a similar formula can be written using cosines (sometimes called the spherical law of cosines, not to be confused with the law of cosines for plane geometry) instead of haversines, but if the two points are close together (e.g. a kilometer apart, on the Earth) you might end up with cos (d/R) = 0.99999999, leading to an inaccurate answer. Since the haversine formula uses sines it avoids that problem.
Either formula is only an approximation when applied to the Earth, which is not a perfect sphere: the "Earth radius" R varies from 6356.78 km at the poles to 6378.14 km at the equator. More importantly, the radius of curvature of a north-south line on the earth's surface is 1% greater at the poles than at the equator— so the haversine formula and law of cosines can't be guaranteed correct to better than 0.5%. More accurate methods that consider the Earth's ellipticity are given by Vincenty's formulae and the other formulas in the geographical distance article.
The law of haversines
Given a unit sphere, a "triangle" on the surface of the sphere is defined by the great circles connecting three points u, v, and w on the sphere. If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the law of haversines states:
Since this is a unit sphere, the lengths a, b, and c are simply equal to the angles (in radians) subtended by those sides from the center of the sphere (for a non-unit sphere, each of these arc lengths is equal to its central angle multiplied by the radius of the sphere).
In order to obtain the haversine formula of the previous section from this law, one simply considers the special case where u is the north pole, while v and w are the two points whose separation d is to be determined. In that case, a and b are π/2 − φ1,2 (i.e., 90° − latitude), C is the longitude separation Δλ, and c is the desired d/R. Noting that sin(π/2 − φ) = cos(φ), the haversine formula immediately follows.
To derive the law of haversines, one starts with the spherical law of cosines:
As mentioned above, this formula is an ill-conditioned way of solving for c when c is small. Instead, we substitute the identity that cos(θ) = 1 − 2 haversin(θ), and also employ the addition identity cos(a − b) = cos(a) cos(b) + sin(a) sin(b), to obtain the law of haversines, above.
References
- U. S. Census Bureau Geographic Information Systems FAQ, What is the best way to calculate the distance between 2 points? (broken link; content has been mirrored here)
- R. W. Sinnott, "Virtues of the Haversine", Sky and Telescope 68 (2), 159 (1984).
- Deriving the haversine formula, Ask Dr. Math (Apr. 20–21, 1999).
- Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).
- W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).
- Oxford English Dictionary. Oxford University Press. 2nd ed. 1989. Cites coinage of term "Haversine" by Prof. Jas. Inman, D. D., in his Navigation and Nautical Astronomy, 3rd ed. (1835).
External links
- The Haversine formula implemented in 9 languages
- JavaScript implementation of Haversine formula to find distance between two latitude/longitude points
- C++ implementation of Haversine formula to find distance between two latitude/longitude points
- Ruby implementation of Haversine formula to find distance between two latitude/longitude points
- Python implementation of Haversine formula to find distance between two latitude/longitude points
- MacOS C implementation of Haversine formula to find distance between two latitude/longitude points using postal zip codes
- Pascal implementation of Haversine formula to find distance between two latitude/longitude points
- Matlab implementation of Haversine formula to find distance between two latitude/longitude points