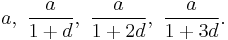Harmonic progression (mathematics)

For the musical term, see Chord progression.

In mathematics, a harmonic progression is a progression formed by taking the reciprocals of an arithmetic progression. In other words, it is a sequence of the form

a,\ \frac{a}{1%2Bd},\ \frac{a}{1%2B2d},\ \frac{a}{1%2B3d}.

where −1/d is not a natural number. Equivalently, a sequence is a harmonic progression when each term is the harmonic mean of the neighboring terms.

Examples are

12, 6, 4, 3, 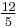\tfrac{12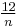}{5}, 2, … , \tfrac{12}{n}
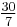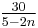
10, 30, −30, −10, −6, − \tfrac{30}{7}, … , \tfrac{30}{5-2n}

Use in geometry

If collinear points A, B, C, and D are such that D is the harmonic conjugate of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression.[1][2] Specifically, each of the sequences AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.

See also

References

  1. ^ Chapters on the modern geometry of the point, line, and circle, Vol. II‎ by Richard Townsend (1865) p. 24
  2. ^ Modern geometry of the point, straight line, and circle: an elementary treatise by John Alexander Third (1898) p. 44