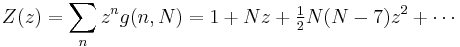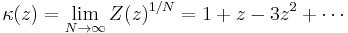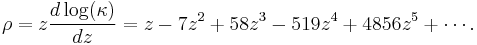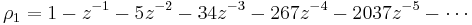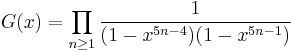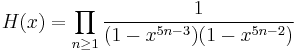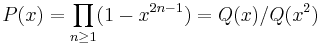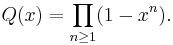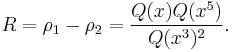Hard hexagon model

In statistical mechanics, the hard hexagon model is a 2-dimensional lattice model of a gas, where particles are allowed to be on the vertices of a triangular lattice but no two particles may be adjacent.

The model was solved by Baxter (1980), who found that it was related to the Rogers-Ramanujan identities.

Contents

The partition function of the hard hexagon model

For a triangular lattice with N sites, the partition function is

\displaystyle Z(z) = \sum_n z^n g(n,N) = 1%2BNz%2B \tfrac{1}{2}N(N-7)z^2%2B\cdots

where g(n, N) is the number of ways of placing n particles on distinct lattice sites such that no 2 are adjacent. The variable z is called the activity and larger values correspond roughly to denser configurations. The function κ is defined by

\kappa(z) = \lim_{N\rightarrow\infty} Z(z)^{1/N} = 1%2Bz-3z^2%2B\cdots

so that log(κ) is the free energy per unit site. Solving the hard hexagon model means (roughly) finding an exact expression for κ as a function of z.

The mean density ρ is given for small z by

\rho= z\frac{d\log(\kappa)}{dz} =z-7z^2%2B58z^3-519z^4%2B4856z^5%2B\cdots.

The vertices of the lattice fall into 3 classes numbered 1, 2, and 3, given by the 3 different ways to fill space with hard hexagons. There are 3 local densities ρ1, ρ2, ρ3, corresponding to the 3 classes of sites. When the activity is large the system approximates one of these 3 packings, so the local densities differ, but when the activity is below a critical point the three local densities are the same. The critical point separating the low-activity homogeneous phase from the high-activity ordered phase is zc = (11 + 53/2)/2 = 11.0917.... Above the critical point the local densities differ and in the phase where most hexagons are on sites of type 1 can be expanded as

\rho_1 = 1-z^{-1}-5z^{-2}-34z^{-3}-267z^{-4}-2037z^{-5}-\cdots
\rho_2=\rho_3 = z^{-2} %2B 9z^{-3} %2B 80z^{-4} %2B 965z^{-5}-\cdots.

Solution

The solution is given for small values of z < zc by

\displaystyle z=\frac{-xH(x)^5}{G(x)^5}
\kappa = \frac{H(x)^3 Q(x^5)^2} {G(x)^2} \prod_{n\ge 1} \frac{(1-x^{6n-4})(1-x^{6n-3})^2(1-x^{6n-2})} {(1-x^{6n-5})(1-x^{6n-1})(1-x^{6n})^2}
\rho =\rho_1=\rho_2=\rho_3= \frac{-xG(x)H(x^6)P(x^3)}{P(x)}

where

G(x) = \prod_{n\ge 1}\frac{1}{(1-x^{5n-4})(1-x^{5n-1})}
H(x) = \prod_{n\ge 1}\frac{1}{(1-x^{5n-3})(1-x^{5n-2})}
P(x) = \prod_{n\ge 1}(1-x^{2n-1}) = Q(x)/Q(x^2)
Q(x) = \prod_{n\ge 1}(1-x^n).

For large z > zc the solution (in the phase where most occupied sites have type 1) is given by

\displaystyle z=\frac{G(x)^5}{xH(x)^5}
\kappa = \frac{G(x)^3 Q(x^5)^2} {H(x)^2} \prod_{n\ge 1} \frac{(1-x^{3n-2})(1-x^{3n-1})} {(1-x^{3n})^2}
\rho_1 = \frac{H(x)Q(x)(G(x)Q(x)%2Bx^2H(x^9)Q(x^9))}{Q(x^3)^2}
\rho_2=\rho_3 = \frac{x^2H(x)Q(x)H(x^9)Q(x^9)}{Q(x^3)^2}
R=\rho_1-\rho_2= \frac{Q(x)Q(x^5)}{Q(x^3)^2}.

The functions G and H turn up in the Rogers-Ramanujan identities, and the function Q is more or less the Dedekind eta function. If x = e2πiτ, then q−1/60G(x), x11/60H(x), x−1/24P(x), z, κ, ρ, ρ1, ρ2, and ρ3 are modular functions of τ, while x1/24Q(x) is a modular form of weight 1/2. Since any two modular functions are related by an algebraic relation, this implies that the functions κ, z, R, ρ are all algebraic functions of each other (of quite high degree) (Joyce 1988).

References

External links