Gyrobifastigium
| Gyrobifastigium | |
|---|---|
| Type | Johnson J25 - J26 - J27 |
| Faces | 4 triangles 4 squares |
| Edges | 14 |
| Vertices | 8 |
| Vertex configuration | 4(3.42) 4(3.4.3.4) |
| Symmetry group | D2d |
| Dual polyhedron | - |
| Properties | convex, honeycomb |
| Net | |
In geometry, the gyrobifastigium is the 26th Johnson solid (J26). It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a half-turn to one prism.
The name comes from the Latin fastigium, meaning a sloping roof.[1] In the standard naming convention of the Johnson solids, bi- means two solids connected at their bases, and gyro- means the two halves are twisted with respect to each other.
The gyrobifastigium's place in the list of Johnson solids, immediately before the bicupolas, is explained by viewing it as a digonal gyrobicupola. Just as the other regular cupolas have an alternating sequence of squares and triangles surrounding a single polygon at the top (triangle, square or pentagon), each half of the gyrobifastigium consists of just alternating squares and triangles, connected at the top only by a ridge.
The gyrobifastigium is one of five convex polyhedra with regular faces capable of space-filling (the others being the cube, truncated octahedron, triangular and hexagonal prism) and it is the only Johnson solid capable of doing so.[2][3][4] The 92 Johnson solids were named and described by Norman Johnson in 1966.
Formulae
The following formulae for volume and surface area can be used if all faces are regular, with edge length a:[5]
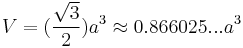
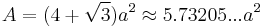
Dual polyhedron
The dual of the gyrobifastigium has 8 faces: 4 isoceles triangles, and 4 parallelograms.
| Dual gyrobifastigium |
|---|
References
- ^ William Smith, D.C.L., LL.D.: A Dictionary of Greek and Roman Antiquities, John Murray, London, 1875
- ^ Weisstein, Eric W., "Space-Filling Polyhedron" from MathWorld.
- ^ Weisstein, Eric W., "Johnson solid" from MathWorld.
- ^ Weisstein, Eric W., "Gyrobifastigium" from MathWorld.
- ^ Stephen Wolfram, "Gyrobifastigium" from Wolfram Alpha. Retrieved July 21, 2010.