Guillaume Amontons
| Guillaume Amontons | |
|---|---|
| Born | 31 August 1663 Paris, France |
| Died | 11 October 1705 Paris |
| Nationality | French |
| Fields | Physics |
| Known for | Tribology |
Guillaume Amontons (31 August 1663 – 11 October 1705) was a French scientific instrument inventor and physicist. He was one of the pioneers in tribology, apart from Leonardo da Vinci, John Theophilus Desaguliers, Leonard Euler and Charles-Augustin de Coulomb.
Contents |
Life
Guillaume was born in Paris, France. His father was a lawyer from Normandy who had moved to the French capital. While still young, Guillaume lost his hearing, which may have motivated him to focus entirely on science. He never attended a university, but was able to study mathematics, the physical sciences, and celestial mechanics. He also spent time studying the skills of drawing, surveying, and architecture.
Work
He was supported in his research career by the government, and was employed in various public works projects.
Scientific instruments
Among his contributions to scientific instrumentation were improvements to the barometer (1695), hygrometer (1687), and thermometer (1695), particularly for use of these instruments at sea. He also demonstrated an optical telegraph and proposed the use of his clepsydra[1] (water clock) for keeping time on a ship at sea.
Thermodynamics
Amontons investigated the relationship between pressure and temperature in gases though he lacked accurate and precise thermometers. Though his results were at best semi-quantitative, he established that the pressure of a gas increases by roughly one-third between the temperatures of cold and the boiling point of water.[2] This was a substantial step towards the subsequent gas laws and, in particular, Charles's law.
His work led him to speculate that a sufficient reduction in temperature would lead to the disappearance of pressure. Thus, he is the first researcher to discuss the concept of an absolute zero of temperature, a concept later extended and rationalised by William Thomson, 1st Baron Kelvin.
Friction
In 1699, Amontons published his rediscovery of the laws of friction first put forward by Leonardo da Vinci.[3] Though they were received with some scepticism, the laws were verified by Charles-Augustin de Coulomb in 1781.[4]
Amontons' Laws of Friction
Amontons' Laws of Friction, first explored by Leonardo da Vinci but never published, were rediscovered and first recorded in print during the late 17th century.
There 3 laws of friction are:[5]
- 1. The force of friction is directly proportional to the applied load. (Amontons 1st Law)
- 2. The force of friction is independent of the apparent area of contact. (Amontons 2nd Law)
- 3. Kinetic friction is independent of the sliding velocity. (Coulomb's Law)
NOTE: These 3 laws only apply to dry friction, in which the addition of a lubricant modifies the tribological properties signifiantly.
Explaining Friction
By looking at any surface on the microscopic level, one would find that it is never perfectly flat. There would exist many tiny bumps and craters, due to imperfections on the surface and the alignment of molecules. (The skin does not feel the bumps and craters because they are too small to be detected.) Considering a smooth stone on a smooth flat road, the two surfaces would be still in contact, but only at a few points (the bumps do not fit exactly into the craters). Due to electrostatic forces of repulsion between the atoms(nuclei against nuclei and electrons against electrons) of the stone and the road, the road will exert a force on the stone, and the stone will exert a force on the road (normal contact forces). The force exerted on the stone would be the NORMAL contact force.
If an external force cause the stone to move to the RIGHT, the forces that the road exert on the stone would be slightly skewed to the LEFT, thus the net force from the road on the stone will be pointing UP but LEFTWARD from the sum of all of the electrostatic forces(tilted contact force). As the vertical component of the net force is the normal contact force, the extra horizontal leftward component of the force would therefore be the FRICTIONAL force. (Note: friction force OPPOSES sliding of two surfaces in contact. On a macro level you could not walk forward without friction pushing you forward)
Amontons First Law Explained
Suppose the stone had a greater mass (hence greater weight as g=constant). The stone would then:
- exert a greater force on the road (the increased load causes the separation distance of the nuclei to decrease, force of repulsion becomes stronger(inverse-square law) ), AND
- more of the atoms of the road and the stone would be in contact.
Hence, when the stone is moved, a greater frictional force would be produced (more areas of contact means that more forces can be skewed, producing more horizontal components of the contact forces).
Amontons law applies to any 2 surfaces, regardless of their orientation. (e.g. pressing a brick against the ceiling, etc.)
NOTE: Applied load means the normal contact force acting on the stone. That is, if the stone is being pushed down harder while it was trying to move, the force acting on the ground increases, and hence the force of the ground acting on the stone (normal contact) increases. This means that more force is required to move the stone across the ground. (frictional force increase)
Amontons Second Law Explained
What this law means is that if two equal masses made of similar material are resting on the same surface with different areas of contact, they would require the same amount of force to start moving (overcome static friction) and to move at constant speed.
To put it in another way: considering 2 equal masses, and the area in contact in situation A is greater than in situation B. This only means that in situation A, the load is distributed across a greater area then in situation B. However, the applied load is still the same! Thus to move both masses, we would require the same amount of applied force to overcome friction. (Amontons First Law)
In summary
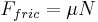 ,
,
where μ is the coefficient of friction and N is the normal contact force.
This is as predicted by Amontons' two laws, where Ffric depends only on the normal contact force (reaction pair of the applied load), and is independent of the surface area in contact.
However, exceptions to Amontons' Law have been observed in various nanometric scenarios. For example, when two surfaces get close enough such that molecular interactions and atomic forces come into play, the two surfaces are attracted together and form what was known as 'negative load'.[6]
Honours
- Member, Académie des Sciences, (1690)
- The crater Amontons on the Moon is named after him.
See also
Notes
- ^ Amontons, G. (1695) Remarques et expériences physiques sur la construction d'une nouvelle clepsydre, Paris.
- ^ - (1699) "Method of substituting the force of fire for horse and man power to move machines", Histoire et Mémoires de l'Académie Royale des Sciences, p.112
- ^ - (1699) Histoire de l'Académie Royale des Sciences avec les Mémoires de Mathématique et de Physique, p.206
- ^ Bowden, F.P. & Tabor, D. (1950) The Friction and Lubrication of Solids pp1, 87-89
- ^ Introduction to Tribology - Friction
- ^ Everything2.com(source may not be reliable)
Further reading
- Asimov's Biographical Encyclopedia of Science and Technology, Isaac Asimov, Doubleday & Co., Inc., 1972, ISBN 0-385-17771-2.
- Cardwell, D.S.L. (1971). From Watt to Clausius: The Rise of Thermodynamics in the Early Industrial Age. Heinemann. ISBN 0-435-54150-1., pp18-19
External links
- The Galileo Project entry on which this biography is partly based.
- Short biography, NNDB page