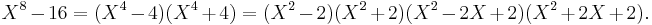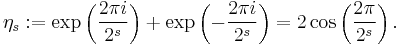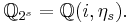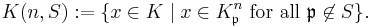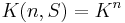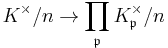Grunwald–Wang theorem
In algebraic number theory, the Grunwald–Wang theorem states that—except in some precisely defined exceptional cases—an element x in a number field K is an nth power in K if it is an nth power in the localization 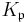 for almost all (i.e. all but finitely many) primes
for almost all (i.e. all but finitely many) primes 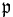 of K. For example, a rational number is a square of a rational number if it is a square of a p-adic number for almost all primes p. The Grunwald–Wang theorem is an example of a local-global principle.
of K. For example, a rational number is a square of a rational number if it is a square of a p-adic number for almost all primes p. The Grunwald–Wang theorem is an example of a local-global principle.
It was introduced by Wilhelm Grunwald (1933), but there was a mistake in this original version that was found and corrected by Shianghao Wang (1948).
Contents |
History
Some days later I was with Artin in his office when Wang appeared. He said he had a counterexample to a lemma which had been used in the proof. An hour or two later, he produced a counterexample to the theorem itself... Of course he [Artin] was astonished, as were all of us students, that a famous theorem with two published proofs, one of which we had all heard in the seminar without our noticing anything, could be wrong.
Grunwald (1933), a student of Hasse, "proved" the erroneous statement that an element in a number field is an nth power if it is an nth power locally almost everywhere. Whaples (1942) gave another "proof" of this incorrect statement. However Wang (1948) discovered the following counter-example: 16 is a p-adic 8th power for all odd primes p, but not a rational (or 2-adic) 8th power. In his doctoral thesis Wang (1950) written under Artin, Wang gave and proved the correct formulation of Grunwald's theorem. This result is what is now known as the Grunwald–Wang theorem. The history of Wang's counterexample is discussed in Roquette (2005, section 5.3)
Proof of Wang's counter-example
It is clear that 16 is not a 2-adic 8th power, and hence not a rational 8th power, since the 2-adic valuation of 16 is 4 which is not divisible by 8.
Generally, 16 is an 8th power in a field K if and only if the polynomial 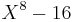 has a root in K. Write
has a root in K. Write
Thus, 16 is an 8th power in K if and only if 2, −2 or −1 is a square in K. Let p be any odd prime. It follows from the multiplicativity of the Legendre symbol that 2, −2 or −1 is a square modulo p. Hence, by Hensel's lemma, 2, −2 or −1 is a square in 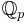 .
.
Another counter-example
16 is not an 8th power in 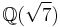 although it is an 8th power locally everywhere (i.e. in
although it is an 8th power locally everywhere (i.e. in 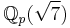 for all p). This follows from the above and the equality
for all p). This follows from the above and the equality 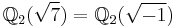 .
.
A consequence of Wang's counter-example
Wang's counter-example has the following interesting consequence showing that one cannot always find a cyclic Galois extension of a given degree of a number field in which finitely many given prime places split in a specified way:
There exists no cyclic degree 8 extension 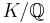 in which the prime 2 is totally inert (i.e. such that
in which the prime 2 is totally inert (i.e. such that 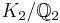 has degree 8).
has degree 8).
Special fields
For any 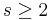 let
let
Note that the 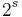 th cyclotomic field is
th cyclotomic field is
A field is called s-special if it contains 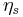 , but neither
, but neither  ,
, 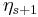 nor
nor 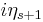 .
.
Statement of the theorem
Consider a number field K and a natural number n. Let S be a finite (possibly empty) set of primes of K and put
The Grunwald–Wang theorem says that
unless we are in the special case which occurs when the following two conditions both hold:
 is s-special with an
is s-special with an  such that
such that 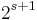 divides n.
divides n. contains the special set
contains the special set 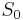 consisting of those (necessarily 2-adic) primes
consisting of those (necessarily 2-adic) primes 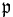 such that
such that 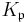 is s-special.
is s-special.
The failure of the Hasse principle is finite: In the special case, the kernel of
is Z/2.
Explanation of Wang's counter-example
The field of rational numbers 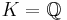 is 2-special since it contains
is 2-special since it contains 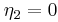 , but neither
, but neither  ,
, 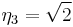 nor
nor 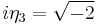 . The special set is
. The special set is 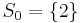 . Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in
. Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in 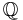 is an nth power if it is a p-adic nth power for all p.
is an nth power if it is a p-adic nth power for all p.
The field 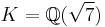 is 2-special as well, but with
is 2-special as well, but with 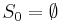 . This explains the other counter-example above.[1]
. This explains the other counter-example above.[1]
Notes
- ^ See Chapter X of Artin–Tate.
References
- Artin, Emil; Tate, John (1990), Class field theory, ISBN 978-0-8218-4426-7, MR0223335, http://books.google.com/books?isbn=978-0-8218-4426-7
- Grunwald, W. (1933), "Ein allgemeiner Existenzsatz für algebraische Zahlkörper", Journal für die reine und angewandte Mathematik 169: 103–107, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002172518
- Roquette, Peter (2005), The Brauer-Hasse-Noether theorem in historical perspective, Schriften der Mathematisch-Naturwissenschaftlichen Klasse der Heidelberger Akademie der Wissenschaften [Publications of the Mathematics and Natural Sciences Section of Heidelberg Academy of Sciences], 15, Berlin, New York: Springer-Verlag, ISBN 978-3-540-23005-2, http://rzuser.uni-heidelberg.de/~ci3/brhano.pdf
- Wang, Shianghaw (1948), "A counter-example to Grunwald's theorem", Annals of Mathematics. Second Series 49: 1008–1009, ISSN 0003-486X, JSTOR 1969410, MR0026992
- Wang, Shianghaw (1950), "On Grunwald's theorem", Annals of Mathematics. Second Series 51: 471–484, ISSN 0003-486X, JSTOR 1969335, MR0033801
- Whaples, George (1942), "Non-analytic class field theory and Grünwald's theorem", Duke Mathematical Journal 9 (3): 455–473, ISSN 0012-7094, MR0007010, http://projecteuclid.org/euclid.dmj/1077493374