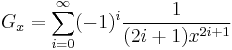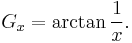Gregory number
In mathematics, a Gregory number, named after James Gregory, is a real number of the form:[1]
where x is any rational number greater or equal to 1. Considering the power series expansion for arctangent, we have
Setting x = 1 gives the well-known Leibniz formula for pi.
See also
References
- ^ Conway, John H.; R. K. Guy (1996). The Book of Numbers. New York: Copernicus Press. pp. 241–243.