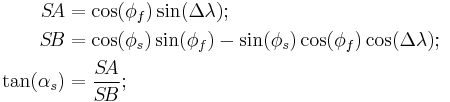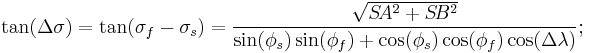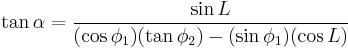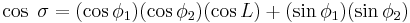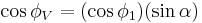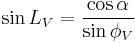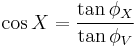Great-circle navigation

Great-circle navigation is the practice of navigating a vessel (such as a ship or aircraft) along a track that follows a great circle. A great circle track is the shortest distance between two points on the surface of a planetary body, assuming a perfect spherical model.

Contents

Methods

In order to construct a great circle track, the navigator of a ship may employ several methods.

Gnomonic chart

A straight line drawn on this chart would represent a great circle track. When this is transferred to a Mercator chart, it becomes a curve. The positions are transferred at a convenient interval of longitude and this is plotted on the Mercator chart with the appropriate latitude.

Spherical trigonometry

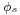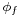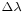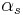If a navigator begins at latitude \scriptstyle\phi_s\,\! (the "standpoint") and plans to travel the great circle to a point at latitude \scriptstyle\phi_f\,\! (the "forepoint"), with a longitude difference between the points of \scriptstyle\Delta\lambda\,\! (positive eastward), his initial course \alpha_s\,\! is given by

\begin{align}S\!A&=\cos(\phi_f)\sin(\Delta\lambda);\\ S\!B&=\cos(\phi_s)\sin(\phi_f)-\sin(\phi_s)\cos(\phi_f)\cos(\Delta\lambda);{}_{\color{white}.}\\ \tan(\alpha_s)&=\frac{S\!A}{S\!B};{}_{\color{white}.}\end{align}\,\!

The central angle between the two points, 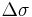\Delta\sigma , is given by

\tan(\Delta\sigma)=\tan(\sigma_f-\sigma_s)=\frac{\sqrt{S\!A^2%2BS\!B^2}}{\sin(\phi_s)\sin(\phi_f)%2B\cos(\phi_s)\cos(\phi_f)\cos(\Delta\lambda)};{}_{\color{white}.}\,\!

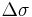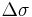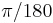which involves the spherical law of cosines. The distance along the great circle will then be \Delta\sigma times the assumed earth radius, where \Delta\sigma is in radians-- that is, degrees multiplied by \pi / 180 .

The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance article.

Other formulas of spherical trigonometry give the latitudes at which the great circle crosses specified longitudes (or vice versa) or the lat-lons of points at specified distance intervals along the great circle.

Spherical Trig (the simple version)

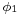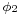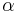A navigator starting at latitude \scriptstyle\phi_1\,\! plans to travel the great circle to a point at latitude \scriptstyle\phi_2\,\!, with a longitude difference between the points of L (positive eastward). His initial course \alpha\,\! is given by

\tan \alpha = \frac{\sin L}{(\cos \phi_1)(\tan \phi_2)- (\sin\phi_1)(\cos L)}


The central angle \sigma between the two points is given by

\cos \;\sigma = (\cos \phi_1)(\cos \phi_2)(\cos L) %2B (\sin \phi_1)(\sin \phi_2)

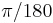The distance along the great circle will then be \sigma times the assumed earth radius, where \sigma is in radians-- that is, degrees multiplied by \pi / 180 .

The earth's actual radius of curvature varies by 1%, so this calculated distance might well be off by a few tenths of a percent; if that's not good enough the navigator can use the ellipsoid-surface formulas in the geographical distance article.

If the central angle is very close to zero or 180 degrees-- if the origin and destination are, say, a kilometer apart, or 19999 kilometers apart-- then the cosine of the central angle will be 0.99999999 or thereabouts, leading to some inaccuracy. The more complicated formulas above are intended to cover that situation and are otherwise unnecessary.

To find the lat-lons of points along the great circle, might as well first calculate the latitude and longitude of the vertex

\cos \phi_V = (\cos \phi_1)(\sin \alpha) \,

\sin L_V = \frac{\cos \alpha}{\sin \phi_V}

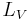where L_V is the difference in longitude between the navigator's starting point and the vertex. Then

\cos X = \frac {\tan \phi_X}{\tan \phi_V}

The great circle crosses latitude 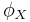\phi_X at longitude X east or west of the vertex. For example, if the vertex is at latitude 45 deg then the great circle crosses latitude 44 degrees at longitudes 15.05 deg east and west of the vertex. (All these formulas assume a spherical earth, of course; no chance formulas for the spheroid would be this simple.)

Computer software

Software is available that allows a navigator to input a departure ("standpoint") and arrival ("forepoint") position to create a list of waypoints which follow a great circle track. Normally, such programs will also calculate the total distance, the distance between successive waypoints, and the courses to be followed between successive waypoints.

See also

Resources