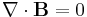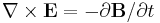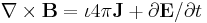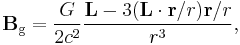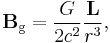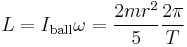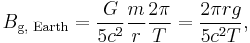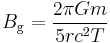Gravitomagnetism

Gravitomagnetism (sometimes Gravitoelectromagnetism, abbreviated GEM), refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test particles. The equations were first published in 1893, before general relativity, by Oliver Heaviside as a separate theory expanding Newton's law.^[1]

1 Background
2 Equations
- 2.1 Lorentz force
- 2.2 In Planck units
3 Higher-order effects
4 Gravitomagnetic fields of astronomical objects
- 4.1 Earth
- 4.2 Pulsar
5 Fringe physics
6 See also
7 References
8 Further reading
9 External links

Background

Gravitomagnetism - Gravitomagnetic field due to angular momentum. (L = angular momentum and H = gravitomagnetic field strength).

Electromagnetism - Magnetic field due to a dipole moment...

...or equivalently current, same field profile, and field generation due to rotation. (B = magnetic induction field, I = current, m = magnetic dipole moment).

Fluid mechanics - Rotational fluid drag of a solid sphere immersed in fluid, analogous directions and senses of rotation as magnetism, analogous interaction to frame dragging for the gravitomagnetic interaction.

Physical analogues of fields.^[2]

This approximate reformulation of gravitation as described by general relativity makes an apparent force appear in a frame of reference different from a freely moving, gravitating body. By analogy with electromagnetism, this apparent force is called the gravitomagnetic force, since it arises in the same way that a moving electric charge creates a magnetic field, the analogous force in special relativity. The main consequence of the gravitomagnetic force, or acceleration, is that a free-falling object near a massive rotating object will itself rotate. This prediction, often loosely referred to as a gravitomagnetic effect, is among the last basic predictions of general relativity yet to be directly tested.

Indirect validations of gravitomagnetic effects have been derived from analyses of relativistic jets. Roger Penrose had proposed a frame dragging mechanism for extracting energy and momentum from rotating black holes.^[3] Reva Kay Williams, University of Florida, developed a rigorous proof that validated Penrose's mechanism.^[4] Her model showed how the Lense-Thirring effect could account for the observed high energies and luminosities of quasars and active galactic nuclei; the collimated jets about their polar axis; and the asymmetrical jets (relative to the orbital plane).^[5] All of those observed properties could be explained in terms of gravitomagnetic effects.^[6] Williams’ application of Penrose's mechanism can be applied to black holes of any size.^[7] Relativistic jets can serve as the largest and brightest form of validations for gravitomagnetism.

A group at Stanford University is currently analyzing data from the first direct test of GEM, the Gravity Probe B satellite experiment, to see if they are consistent with gravitomagnetism. The Apache Point Observatory Lunar Laser-ranging Operation also plans to observe gravitomagnetism effects.

Equations

According to general relativity, the gravitational field produced by a rotating object (or any rotating mass-energy) can, in a particular limiting case, be described by equations that have the same form as the magnetic field in classical electromagnetism. Starting from the basic equation of general relativity, the Einstein field equation, and assuming a weak gravitational field or reasonably flat spacetime, the gravitational analogs to Maxwell's equations for electromagnetism, called the "GEM equations", can be derived. GEM equations compared to Maxwell's equations in SI units are:^[8]^[9] ^[10]^[11]^[12]

GEM equations	Maxwell's equations
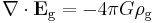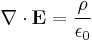$\nabla \cdot \mathbf{E}_\text{g} = -4 \pi G \rho_\text{g} \$	$\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}$
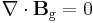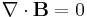$\nabla \cdot \mathbf{B}_\text{g} = 0 \$	$\nabla \cdot \mathbf{B} = 0 \$
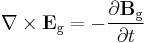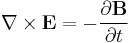$\nabla \times \mathbf{E}_\text{g} = -\frac{\partial \mathbf{B}_\text{g} } {\partial t} \$	$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B} } {\partial t} \$
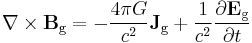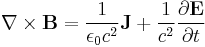$\nabla \times \mathbf{B}_\text{g} = -\frac{4 \pi G}{c^2} \mathbf{J}_\text{g} %2B \frac{1}{c^2} \frac{\partial \mathbf{E}_\text{g}} {\partial t}$	$\nabla \times \mathbf{B} = \frac{1}{\epsilon_0 c^2} \mathbf{J} %2B \frac{1}{c^2} \frac{\partial \mathbf{E}} {\partial t}$

where:

E_g is the static gravitational field (conventional gravity, also called gravitoelectric in analogous usage);
E is the electric field;
B_g is the gravitomagnetic field;
B is the magnetic field;
ρ_g is mass density;
ρ is charge density:
J_g is mass current density (J_g = ρ_g v_ρ, where v_ρ is the velocity of the mass flow generating the gravitomagnetic field);
J is electric current density;
G is the gravitational constant;
ε₀ is the vacuum permittivity;
c is the speed of propagation of gravity (which is equal to the speed of light according to general relativity).

Lorentz force

For a test particle whose mass m is "small", in a stationary system, the net (Lorentz) force acting on it due to a GEM field is described by the following GEM analog to the Lorentz force equation:

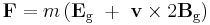$\mathbf{F} = m \left( \mathbf{E}_\text{g} \ %2B \ \mathbf{v} \times 2 \mathbf{B}_\text{g} \right)$ .

where:

m is the mass of the test particle;
v is the instantaneous velocity of the test particle.

The acceleration of any test particle is simply:

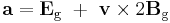$\mathbf{a} = \mathbf{E}_\text{g} \ %2B \ \mathbf{v} \times 2 \mathbf{B}_\text{g}$ .

In some literature, all instances of B_g in the GEM equations are multiplied by 1/2, a factor absent from Maxwell's equations. This factor vanishes if B_g in the GEM version of the Lorentz force equation is multiplied by 2, as shown above. The factors 2 or 1/2 arise because the gravitational field is caused by the stress-energy tensor which is a second rank tensor, as opposed to the electromagnetic field which is caused by the four-current, a first rank tensor. This difference becomes intuitively clear when one compares non-invariance of relativistic mass to electric charge invariance. This is often referred to as gravity being a spin-2 field and electromagnetism being a spin-1 field.

In Planck units

From comparison of GEM equations and Maxwell's equations it is obvious that −1/(4πG) is the gravitational analog of vacuum permittivity ε₀. Adopting Planck units normalizes G, c and 1/(4πε₀) to 1, thereby eliminating these constants from both sets of equations. The two sets of equations then become identical but for the minus sign preceding 4π in the GEM equations. These minus signs stem from an essential difference between gravity and electromagnetism: electrostatic charges of identical sign repel each other, while masses attract each other. Hence the GEM equations are simply Maxwell's equations with mass (or mass density) substituting for charge (or charge density), and −G replacing the Coulomb force constant 1/(4πε₀).

The following Table summarizes the results thus far:

Common Structure of the Maxwell and GEM Equations Given Planck units.
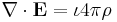
$\nabla \cdot \mathbf{E} = \iota 4\pi\rho$ $\nabla \cdot \mathbf{B} = 0$ $\nabla \times \mathbf{E} = -\partial \mathbf{B}/ \partial t$ $\nabla \times \mathbf{B} = \iota 4\pi\mathbf{J} %2B \partial \mathbf{E}/ \partial t$ ι = +1 (Maxwell) or −1 (GEM).

4π appears in both the GEM and Maxwell equations, because Planck units normalize G and 1/(4πε₀) to 1, and not 4πG and 1/ε₀.

Higher-order effects

Some higher-order gravitomagnetic effects can reproduce effects reminiscent of the interactions of more conventional polarized charges. For instance, if two wheels are spun on a common axis, the mutual gravitational attraction between the two wheels will be greater if they spin in opposite directions than in the same direction. This can be expressed as an attractive or repulsive gravitomagnetic component.

Gravitomagnetic arguments also predict that a flexible or fluid toroidal mass undergoing minor axis rotational acceleration (accelerating "smoke ring" rotation) will tend to pull matter through the throat (a case of rotational frame dragging, acting through the throat). In theory, this configuration might be used for accelerating objects (through the throat) without such objects experiencing any g-forces.^[13]

Consider a toroidal mass with two degrees of rotation (both major axis and minor-axis spin, both turning inside out and revolving). This represents a "special case" in which gravitomagnetic effects generate a chiral corkscrew-like gravitational field around the object. The reaction forces to dragging at the inner and outer equators would normally be expected to be equal and opposite in magnitude and direction respectively in the simpler case involving only minor-axis spin. When both rotations are applied simultaneously, these two sets of reaction forces can be said to occur at different depths in a radial Coriolis field that extends across the rotating torus, making it more difficult to establish that cancellation is complete.

Modelling this complex behaviour as a curved spacetime problem has yet to be done and is believed to be very difficult.

Gravitomagnetic fields of astronomical objects

The formula for the gravitomagnetic field B_g near a rotating body can be derived from the GEM equations. It is given by:^[9]

$\mathbf{B}_\text{g} = \frac{G }{2 c^2} \frac{\mathbf{L} - 3(\mathbf{L} \cdot \mathbf{r}/r) \mathbf{r}/r}{r^3},$

where L is the angular momentum of the body. At the equatorial plane, r and L are perpendicular, so their dot product vanishes, and this formula reduces to:

$\mathbf{B}_\text{g} = \frac{G }{2 c^2} \frac{\mathbf{L}}{r^3},$

The magnitude of angular momentum of a homogeneous ball-shaped body is:

$L=I_\text{ball} \omega= \frac{2 m r^2}{5} \frac{2 \pi}{T}$

where:

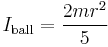$I_\text{ball} = \frac{2 m r^2}{5}$ is the moment of inertia of a ball-shaped body (see: list of moments of inertia);
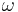$\omega \$ is the angular velocity;
m is the mass;
r is the radius;
T is the rotational period.

Earth

Therefore, the magnitude of Earth's gravitomagnetic field at its equator is:

$B_\text{g, Earth} = \frac{G }{5 c^2} \frac{m}{r} \frac{2 \pi}{T} = \frac{2 \pi r g}{5c^2 T},$

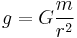where $g = G \frac{m}{r^2}$ is Earth's gravity. The force direction coincides with the angular moment direction, i.e. north.

From this calculation it follows that Earth's equatorial gravitomagnetic field is about 1.012×10⁻¹⁴ Hz,^[14] or 3.1×10⁻⁷ in units of standard gravity (9.81 m/s²) divided by the speed of light. Such a field is extremely weak and requires extremely sensitive measurements to be detected. One experiment to measure such field was the Gravity Probe B mission.

Pulsar

If the preceding formula is used with the second fastest-spinning pulsar known, PSR J1748-2446ad (which rotates 716 times per second), assuming a radius of 16 km, and two solar masses, then

$B_\text{g} = \frac{2 \pi G m}{5rc^2 T}$

equals about 166 Hz. This would be easy to notice. However, the pulsar is spinning at a quarter of the speed of light at the equator, and its radius is only three times more than its Schwarzschild radius. When such fast motion and such strong gravitational fields exist in a system, the simplified approach of separating gravitomagnetic and gravitoelectric forces can be applied only as a very rough approximation.

Fringe physics

Incomplete understanding of the meaning of the similarity of the gravitomagnetic formulas, above, and Maxwell's equations for (real) electricity and magnetism have given rise to fringe physics. Use of the gravitomagnetic analogy for a simplified form of the Einstein field equations, on the other hand, is firmly part of General Relativity. It is an approximation to the current standard theory of gravitation, and has testable predictions, which are in the final stages of being directly tested by the Gravity Probe B experiment. Despite the use of the word magnetism in gravitomagnetism, and despite the similarity of the GEM force laws to the (real) electromagnetic force law, gravitomagnetism should not be confused with any of the following:

Claims to have constructed anti-gravity devices;
Eugene Podkletnov's claims to have constructed gravity-shielding devices and gravitational reflection beams.
Any proposal to produce gravitation using electrical circuits.

References

^ O. Heaviside (1893). "A gravitational and electromagnetic analogy". The Electrician 31: 81–82. http://serg.fedosin.ru/Heavisid.htm.
^ Gravitation and Inertia, I. Ciufolini and J.A. Wheeler, Princeton Physics Series, 1995, ISBN 0-691-03323-4
^ R. Penrose (1969). "Gravitational collapse: The role of general relativity". Rivista de Nuovo Cimento, Numero Speciale 1: 252–276. Bibcode 1969NCimR...1..252P.
^ R.K. Williams (1995). "Extracting x rays, Ύ rays, and relativistic e⁻e⁺ pairs from supermassive Kerr black holes using the Penrose mechanism". Physical Review 51 (10): 5387–5427. Bibcode 1995PhRvD..51.5387W. doi:10.1103/PhysRevD.51.5387.
^ R.K. Williams (2004). "Collimated escaping vortical polar e⁻e⁺ jets intrinsically produced by rotating black holes and Penrose processes". The Astrophysical Journal 611 (2): 952–963. arXiv:astro-ph/0404135. Bibcode 2004ApJ...611..952W. doi:10.1086/422304.
^ R.K. Williams (2005). "Gravitomagnetic field and Penrose scattering processes". Annals of the New York Academy of Sciences. 1045. pp. 232–245.
^ R.K. Williams (2001). "Collimated energy-momentum extraction from rotating black holes in quasars and microquasars using the Penrose mechanism". AIP Conference Proceedings. 586. pp. 448–453.
^ R.P. Lano (1996). "Gravitational Meissner Effect". arXiv:hep-th/9603077 [hep-th].
^ ^a ^b Fedosin S.G. (1999). Fizika i filosofiia podobiia ot preonov do metagalaktik. Perm. p. 544. ISBN 5813100121. http://lccn.loc.gov/2009457349.
^ M. Agop, C. Gh. Buzea, B. Ciobanu (1999). "On Gravitational Shielding in Electromagnetic Fields". arXiv:physics/9911011 [physics.gen-ph].
^ B. Mashhoon, F. Gronwald, H.I.M. Lichtenegger (1999). "Gravitomagnetism and the Clock Effect". Lect.Notes Phys. 562: 83–108. arXiv:gr-qc/9912027. Bibcode 2001LNP...562...83M.
^ S.J. Clark, R.W. Tucker (2000). "Gauge symmetry and gravito-electromagnetism". Classical and Quantum Gravity 17 (19): 4125–4157. arXiv:gr-qc/0003115. Bibcode 2000CQGra..17.4125C. doi:10.1088/0264-9381/17/19/311.
^ R.L. Forward (1963). "Guidelines to Antigravity". American Journal of Physics 31 (3): 166–170. Bibcode 1963AmJPh..31..166F. doi:10.1119/1.1969340.
^ http://www.google.com/search?q=2*pi*radius+of+Earth*earth+gravity%2F(5*c^2*day)