Graph algebra
In mathematics, especially in the fields of universal algebra and graph theory, a graph algebra is a way of giving a directed graph an algebraic structure. It was introduced in (McNulty & Shannon 1983), and has seen many uses in the field of universal algebra since then.
Contents |
Definition
Let 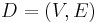 be a directed graph, and let
be a directed graph, and let  be an element not in
be an element not in  . The graph algebra associated with
. The graph algebra associated with  is the set
is the set 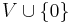 equipped with multiplication defined by the rules
equipped with multiplication defined by the rules 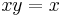 if
if 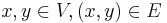 , and
, and 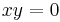 if
if 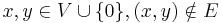 .
.
Applications
This notion has made it possible to use the methods of graph theory in universal algebra and several other directions of [English]] and [[computer scies have been used, for example, in constructions concerning dualities (Davey et al. 2000), equational theories (Pöschel 1989), flatness (Delić 2001), groupoid rings (Lee 1991), topologies (Lee 1988), varieties (Oates-Williams 1984), finite state automata (Kelarev, Miller & Sokratova 2005), finite state machines (Kelarev & Sokratova 2003), tree languages and tree automata (Kelarev & Sokratova 2001) etc.
See also
References
- Davey, Brian A.; Idziak, Pawel M.; Lampe, William A.; McNulty, George F. (2000), "Dualizability and graph algebras", Discrete Mathematics 214 (1): 145–172, doi:10.1016/S0012-365X(99)00225-3, ISSN 0012-365X, MR1743633
- Delić, Dejan (2001), "Finite bases for flat graph algebras", Journal of Algebra 246 (1): 453–469, doi:10.1006/jabr.2001.8947, ISSN 0021-8693, MR1872631
- McNulty, George F.; Shallon, Caroline R. (1983), "Inherently nonfinitely based finite algebras", Universal algebra and lattice theory (Puebla, 1982), Lecture Notes in Math., 1004, Berlin, New York: Springer-Verlag, pp. 206–231, doi:10.1007/BFb0063439, MR716184
- Kelarev, A.V. (2003), Graph Algebras and Automata, New York: Marcel Dekker, ISBN 0-8247-4708-9, MR2064147
- Kelarev, A.V.; Sokratova, O.V. (2003), "On congruences of automata defined by directed graphs", Theoretical Computer Science 301 (1–3): 31–43, doi:10.1016/S0304-3975(02)00544-3, ISSN 0304-3975, MR1975219
- Kelarev, A.V.; Miller, M.; Sokratova, O.V. (2005), "Languages recognized by two-sided automata of graphs", Proc. Estonian Akademy of Science 54 (1): 46–54, ISSN 1736-6046, MR2126358
- Kelarev, A.V.; Sokratova, O.V. (2001), "Directed graphs and syntactic algebras of tree languages", J. Automata, Languages & Combinatorics 6 (3): 305–311, ISSN 1430-189X, MR1879773
- Kiss, E.W.; Pöschel, R.; Pröhle, P. (1990), "Subvarieties of varieties generated by graph algebras", Acta Sci. Math. (Szeged) 54 (1–2): 57–75, MR1073419
- Lee, S.-M. (1988), "Graph algebras which admit only discrete topologies", Congr. Numer. 64: 147–156, ISSN 1736-6046, MR0988675
- Lee, S.-M. (1991), "Simple graph algebras and simple rings", Southeast Asian Bull. Math. 15 (2): 117–121, ISSN 0129-2021, MR1145431
- Oates-Williams, Sheila (1984), "On the variety generated by Murskiĭ's algebra", Algebra Universalis 18 (2): 175–177, doi:10.1007/BF01198526, ISSN 0002-5240, MR743465
- Pöschel, R (1989), "The equational logic for graph algebras", Z. Math. Logik Grundlag. Math. 35 (3): 273–282, doi:10.1002/malq.19890350311, MR1000970
Further reading
- Raeburn, Iain (2005), Graph algebras, American Mathematical Society, ISBN 9780821836606