Graph (abstract data type)

In computer science, a graph is an abstract data type that is meant to implement the graph and hypergraph concepts from mathematics.

A graph data structure consists of a finite (and possibly mutable) set of ordered pairs, called edges or arcs, of certain entities called nodes or vertices. As in mathematics, an edge (x,y) is said to point or go from x to y. The nodes may be part of the graph structure, or may be external entities represented by integer indices or references.

A graph data structure may also associate to each edge some edge value, such as a symbolic label or a numeric attribute (cost, capacity, length, etc.).

1 Algorithms
2 Operations
3 Representations
4 Types
5 See also
6 References
7 Further reading
8 External links

Algorithms

Graph algorithms are a significant field of interest within computer science. Typical higher-level operations associated with graphs are: finding a path between two nodes, like depth-first search and breadth-first search and finding the shortest path from one node to another, like Dijkstra's algorithm. A solution to finding the shortest path from each node to every other node also exists in the form of the Floyd–Warshall algorithm.

A directed graph can be seen as a flow network, where each edge has a capacity and each edge receives a flow. The Ford–Fulkerson algorithm is used to find out the maximum flow from a source to a sink in a graph.

Operations

The basic operations provided by a graph data structure G usually include:

adjacent(G, x, y): tests whether there is an edge from node x to node y.
neighbors(G, x): lists all nodes y such that there is an edge from x to y.
add(G, x, y): adds to G the edge from x to y, if it is not there.
delete(G, x, y): removes the edge from x to y, if it is there.
get_node_value(G, x): returns the value associated with the node x.
set_node_value(G, x, a): sets the value associated with the node x to a.

Structures that associate values to the edges usually also provide:

get_edge_value(G, x, y): returns the value associated to the edge (x,y).
set_edge_value(G, x, y, v): sets the value associated to the edge (x,y) to v.

Representations

Different data structures for the representation of graphs are used in practice:

Adjacency list – Vertices are stored as records or objects, and every vertex stores a list of adjacent vertices. This data structure allows the storage of additional data on the vertices.
Incidence list – Vertices and edges are stored as records or objects. Each vertex stores its incident edges, and each edge stores its incident vertices. This data structure allows the storage of additional data on vertices and edges.
Adjacency matrix – A two-dimensional matrix, in which the rows represent source vertices and columns represent destination vertices. Data on edges and vertices must be stored externally. Only the cost for one edge can be stored between each pair of vertices.
Incidence matrix – A two-dimensional Boolean matrix, in which the rows represent the vertices and columns represent the edges. The entries indicate whether the vertex at a row is incident to the edge at a column.

The following table gives the time complexity cost of performing various operations on graphs, for each of these representations. In the matrix representations, the entries encode the cost of following an edge. The cost of edges that are not present are assumed to be 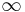$\infty$ .

	Adjacency list	Incidence list	Adjacency matrix	Incidence matrix
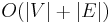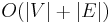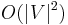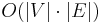Storage	$O(\|V\|%2B\|E\|)$	$O(\|V\|%2B\|E\|)$	$O(\|V\|^2)$	$O(\|V\|\cdot\|E\|)$
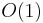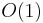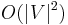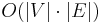Add vertex	$O(1)$	$O(1)$	$O(\|V\|^2)$	$O(\|V\|\cdot\|E\|)$
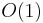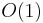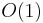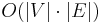Add edge	$O(1)$	$O(1)$	$O(1)$	$O(\|V\|\cdot\|E\|)$
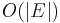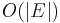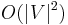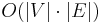Remove vertex	$O(\|E\|)$	$O(\|E\|)$	$O(\|V\|^2)$	$O(\|V\|\cdot\|E\|)$
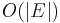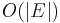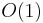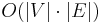Remove edge	$O(\|E\|)$	$O(\|E\|)$	$O(1)$	$O(\|V\|\cdot\|E\|)$
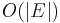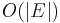Query: are vertices u, v adjacent? (Assuming that the storage positions for u, v are known)	$O(\|E\|)$	$O(\|E\|)$	$O(1)$	$O(\|E\|)$
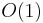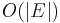Remarks	When removing edges or vertices, need to find all vertices or edges		Slow to add or remove vertices, because matrix must be resized/copied	Slow to add or remove vertices and edges, because matrix must be resized/copied

Adjacency lists are generally preferred because they efficiently represent sparse graphs. An adjacency matrix is preferred if the graph is dense, that is the number of edges E is close to the number of vertices squared, V², or if one must be able to quickly look up if there is an edge connecting two vertices.^[1]

Types

Skip graphs

References

^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw–Hill. ISBN 0-262-53196-8.

External links

Boost Graph Library: a powerful C++ graph library

Data structures

Types	Collection Container

Abstract	List Associative array Multimap Set Multiset Double-ended queue Queue Priority queue Stack

Arrays	Dynamic array Hashed array tree Sparse array Circular buffer Bit array Hash table

Linked	Linked list Unrolled linked list XOR linked list Skip list

Trees	B-tree Binary search tree (self-balancing: AA, AVL, red-black, splay) Heap (binary, binomial, Fibonacci) Trie

Graphs	Directed graph Directed acyclic graph Binary decision diagram Hypergraph

List of data structures