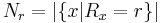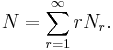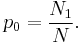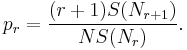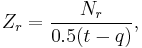Good–Turing frequency estimation
Good–Turing frequency estimation is a statistical technique for predicting the probability of occurrence of objects belonging to an unknown number of species, given past observations of such objects and their species. (In drawing balls from an urn, the 'objects' would be balls and the 'species' would be the distinct colors of the balls (finite but unknown in number). After drawing 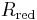 red balls,
red balls, 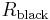 black balls and
black balls and 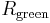 green balls, we would ask what is the probability of drawing a red ball, a black ball, a green ball or one of a previously unseen color.)
green balls, we would ask what is the probability of drawing a red ball, a black ball, a green ball or one of a previously unseen color.)
Contents |
Historical background
Good–Turing frequency estimation was developed by Alan Turing and his assistant I.J. Good as part of their efforts at Bletchley Park to crack German ciphers for the Enigma machine during World War II. Turing at first modeled the frequencies as a binomial distribution, but found it inaccurate. Good developed smoothing algorithms to improve the estimator's accuracy.
The discovery was recognized as significant when published by Good in 1953,[1] but the calculations were difficult so it was not used as widely as it might have been.[2] The method even gained some literary fame due to the Robert Harris novel Enigma.
In the 1990s, Geoffrey Sampson worked with William A. Gale of AT&T, to create and implement a simplified and easier-to-use variant of the Good–Turing method[3] described below.
The method
Some data structures and notation are defined first. Assume that X distinct species have been observed, numbered x = 1, ..., X. The frequency vector, R, has elements 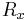 that give the number of individuals that have been observed for species x.
that give the number of individuals that have been observed for species x.
The frequency of frequencies vector, 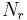 , shows how many times the frequency r occurs in the vector R; i.e. among the elements
, shows how many times the frequency r occurs in the vector R; i.e. among the elements 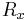 .
.
For example 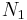 is the number of species for which only 1 individual was observed. Note that the total number of objects observed, N, can be found from
is the number of species for which only 1 individual was observed. Note that the total number of objects observed, N, can be found from
The first step in the calculation is to find an estimate of the total probability of unseen objects. This estimate is[4]
The next step is to find an estimate of probability for objects which were seen r times. This estimate is
Here, the notation 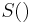 means the smoothed or adjusted value of the frequency shown in parenthesis (see also empirical Bayes method). An overview of how to perform this smoothing follows.
means the smoothed or adjusted value of the frequency shown in parenthesis (see also empirical Bayes method). An overview of how to perform this smoothing follows.
We would like to make a plot of 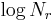 versus
versus 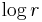 but this is problematic because for large r many
but this is problematic because for large r many 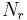 will be zero. Instead a revised quantity,
will be zero. Instead a revised quantity, 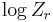 , is plotted versus
, is plotted versus 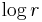 , where Zr is defined as
, where Zr is defined as
and where q, r and t are consecutive subscripts having 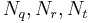 non-zero. When r is 1, take q to be 0. When r is the last non-zero frequency, take t to be 2r-q.
non-zero. When r is 1, take q to be 0. When r is the last non-zero frequency, take t to be 2r-q.
A simple linear regression is then fitted to the log–log plot. For small values of r it is reasonable to set 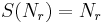 (that is, no smoothing is performed), while for large values of r, values of
(that is, no smoothing is performed), while for large values of r, values of 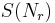 are read off the regression line. An automatic procedure (not described here) can be used to specify at what point the switch from no smoothing to linear smoothing should take place. Code for the method is available in the public domain.[5]
are read off the regression line. An automatic procedure (not described here) can be used to specify at what point the switch from no smoothing to linear smoothing should take place. Code for the method is available in the public domain.[5]
See also
References
- ^ Good, I.J. (1953). "The population frequencies of species and the estimation of population parameters". Biometrika 40 (3–4): 237–264. doi:10.1093/biomet/40.3-4.237. JSTOR 2333344. MR61330.
- ^ Newsise: Scientists Explain and Improve Upon 'Enigmatic' Probability Formula, a popular review of Orlitsky A, Santhanam NP, Zhang J. (2003). "Always Good Turing: asymptotically optimal probability estimation.". Science (New York, N.Y.). 302 (5644): 427–31. doi:10.1126/science.1088284.
- ^ Sampson, Geoffrey (2000) Good–Turing Frequency Estimation
- ^ Gale, William A. (1995). "Good–Turing smoothing without tears". Journal of Quantitative Linguistics 2: 3. doi:10.1080/09296179508590051.
- ^ Sampson, Geoffrey (2005) Simple Good–Turing Frequency Estimator (code in C)
- David A. McAllester, Robert Schapire (2000) On the Convergence Rate of Good–Turing Estimators'', Proceedings of the Thirteenth Annual Conference on Computational Learning Theory pp. 1–6