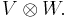Glossary of tensor theory

This is a glossary of tensor theory. For expositions of tensor theory from different points of view, see:

For some history of the abstract theory see also Multilinear algebra.

1 Classical notation
2 Algebraic notation
3 Applications
4 Tensor field theory
5 Abstract algebra
6 Spinors

Classical notation

Tensor order

A tensor written in component form is an indexed array. The order of a tensor is the number of indices required. (The rank of tensor used to mean the order, but now it means something different)

Rank

The rank of the tensor is the minimal number of rank-one tensor that you need to sum up to obtain this higher-rank tensor. Rank-one tensors are given the generalization of outer product to m-vectors where m is the order of the tensor.

Dyadic tensor

A dyadic tensor has order two, and may be represented as a square matrix. The conventions a_ij, a_i^j, and a^ij, do have different meanings (the position of the index determines its valence (variance), in that the first may represent a quadratic form, the second a linear transformation, and the distinction is important in contexts that require tensors that aren't orthogonal (see below). A dyad is a tensor such as a_ib^j, product component-by-component of rank one tensors. In this case it represents a linear transformation, of rank one in the sense of linear algebra - a clashing terminology that can cause confusion.

Einstein notation

This notation is based on the understanding that in a product of two indexed arrays, if an index letter in the first is repeated in the second, then the (default) interpretation is that the product is summed over all values of the index. For example if a_ij is a matrix, then under this convention a_ii is its trace. The Einstein convention is generally used in physics and engineering texts, to the extent that if summation is not to be applied it is normal to note that explicitly.

Kronecker delta

Levi-Civita symbol

Covariant tensor, Contravariant tensor

The classical interpretation is by components. For example in the differential form a_i dx^j the components a_i are a covariant vector. That means all indices are lower; contravariant means all indices are upper.

Mixed tensor

This refers to any tensor with lower and upper indices.

Cartesian tensor

Cartesian tensors are widely used in various branches of continuum mechanics, such as fluid mechanics and elasticity. In classical continuum mechanics, the space of interest is usually 3-dimensional Euclidean space, as is the tangent space at each point. If we restrict the local coordinates to be Cartesian coordinates with the same scale centered at the point of interest, the metric tensor is the Kronecker delta. This means that there is no need to distinguish covariant and contravariant components, and furthermore there is no need to distinguish tensors and tensor densities. All Cartesian-tensor indices are written as subscripts. Cartesian tensors achieve considerable computational simplification at the cost of generality and of some theoretical insight.

Contraction of a tensor

Raising and lowering indices

Symmetric tensor

Antisymmetric tensor

Multiple cross products

Algebraic notation

This avoids the initial use of components, and is distinguished by the explicit use of the tensor product symbol.

Tensor product

If v and w are vectors in vector spaces V and W respectively, then

$v \otimes w \,$

is a tensor in

$V \otimes W. \,$

That is, the $\otimes$ operation is a binary operation, but it takes values into a fresh space (it is in a strong sense external). The $\otimes$ operation is a bilinear map; but no other conditions are applied to it.

Pure tensor

A pure tensor of 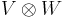$V \otimes W$ is one that is of the form $v \otimes w$ .

It could be written dyadically a_ib_j, or more accurately a_ib_j e_i $\otimes$ f_j, where the e_i are a basis for V and the f_j a basis for W. Therefore, unless V and W have the same dimension, the array of components need not be square. Such pure tensors are not generic: if both V and W have dimension > 1, there will be tensors that are not pure, and there will be non-linear conditions for a tensor to satisfy, to be pure. For more see Segre embedding.

Tensor algebra

In the tensor algebra T(V) of a vector space V, the operation

$\otimes$

becomes a normal (internal) binary operation. This is at the cost of T(V) being of infinite dimension, unless V has dimension 0. The free algebra on a set X is for practical purposes the same as the tensor algebra on the vector space with X as basis.

Hodge star operator

Exterior power

The wedge product is the anti-symmetric form of the $\otimes$ operation. The quotient space of T(V) on which it becomes an internal operation is the exterior algebra of V; it is a graded algebra, with the graded piece of weight k being called the k-th exterior power of V.

Symmetric power, symmetric algebra

This is the invariant way of constructing polynomial algebras.

Applications

Metric tensor

Strain tensor

Stress-energy tensor

Tensor field theory

Jacobian matrix

Tensor field

Tensor density

Lie derivative

Tensor derivative

Differential geometry

Abstract algebra

Tensor product of fields

This is an operation on fields, that does not always produce a field.

Tensor product of R-algebras

Clifford module

A representation of a Clifford algebra which gives a realisation of a Clifford algebra as a matrix algebra.

Tor functors

These are the derived functors of the tensor product, and feature strongly in homological algebra. The name comes from the torsion subgroup in abelian group theory.

Symbolic method of invariant theory

Derived category Grothendieck's six operations

These are highly abstract approaches used in some parts of geometry.

Spinors

See: spin group, spin-c group, spinors, pin group, pinors, spinor field, Killing spinor, spin manifold.